|
Objetivos |Importancia|
Proyección del PEA
|Proyección
en áreas menores | 13. Estimaciones y Proyecciones derivadas de población Objetivos
Las proyecciones de población no constituyen un fin, sino que posterior a ellas se plantea el problema de su utilización como base para la toma de decisiones en diferentes planos: económico, político y social. En este sentido, una vez desarrolladas las proyecciones nacionales de población de un país, surge una serie de necesidades con respecto a otras proyecciones a nivel desagregado y que utilizan como referencia las proyecciones nacionales. Las proyecciones desagregadas más destacadas son: proyecciones urbano-rural, proyección de población económicamente activa, proyecciones de la matrícula escolar, proyecciones regionales, proyecciones de áreas administrativas menores, etc. Las proyecciones por sexo y grupos de edad proporcionan directamente la magnitud de algunos segmentos poblacionales que se requiere analizar su evolución: población femenina en edad fértil, población en edad escolar por sexo, población de personas mayores a los años, población de personas en edad de laborar, etc. Sin embargo, otros sectores requieren de un tratamiento especial. Por ejemplo, en muchos países en desarrollo, existe una clara diferencia entre la población en edad escolar y la matrícula real de asistencia a centros educativos. Esto obliga a conocer y proyectar las tasas de escolaridad para los diferentes niveles educativos. Desde este punto de vista, la demanda de escuelas, colegios, educadores, tecnología, etc. Del mismo modo, la fuerza de trabajo es una combinación entre la población en edad de trabajar y los porcentajes de población de las diferentes edades, que efectivamente laborarán remuneradamente. Los elementos anteriores indican que la elaboración de proyecciones derivadas, además de las proyecciones nacionales de población por sexo y grupos de edad, implican la elaboración de proyecciones sobre ciertos índices relacionados con el fenómeno que se desea predecir, tales como las tasas de escolaridad para las proyecciones de la matricula escolar, los porcentajes de individuos inmersos en el campo laboral para las proyecciones de la fuerza de trabajo, etc. Para la proyección de estos índices es necesario conocer las tendencias que se han presentado en el pasado y el comportamiento que se esperaría para el futuro. Este tipo de proyecciones provee al investigador o planificador, del comportamiento futuro esperado en ausencia de nuevas políticas en este sentido (proyección del pasado); sin embargo, estas proyecciones pueden ser mejoradas notablemente con la consideración de los planes futuros, que en esa materia quiera impulsar un gobierno o el sector privado. Para analizar con mayor detalle la aplicación de estas técnicas, seguidamente se describe, en términos generales, la aplicación de ciertas estrategias básicas para proyectar la población económicamente activa de un país. Proyección de la población económicamente activa: PEA La población económicamente activa "comprende el total de personas de uno u otro sexo de 12 años o más, que suministran la mano de obra disponible para la producción de bienes y servicios". Esto quiere decir, que la PEA está constituida por las personas que conforman la oferta de trabajo de un país o región. Para el análisis de la PEA no solo se debe considerar su magnitud, sino también las variables asociadas tales como: el género, la edad, la distribución regional, la calificación profesional, los niveles de instrucción, etc. Los censos de población y las encuestas especializadas, son las fundamentales fuentes de información para analizar la PEA. Las principales preguntas que se realizan con esta intención son: ¿Tiene actualmente empleo? En caso que trabaje deben incluirse: ¿En qué sector económico trabaja? ¿Cuál es su ocupación? En caso que no trabaje se incluye: ¿Está en busca de empleo actualmente? Los principales errores de este tipo de información están asociados con la omisión de algunas personas, mala declaración de la edad, de la ocupación, etc. Además de estos problemas, se presentan otros asociados con la definición de los conceptos sobre todo en lo que respecta a la actividad que realizan las personas y con su jornada de trabajo. El método utilizado para proyectar la población económicamente activa se fundamenta en los principios básicos del método de componentes, discutido en la sesión anterior. Básicamente la técnica consiste en construir un conjunto de tasas de actividad modelo que se supone se alcanzarán en una fecha determinada. Entonces, al igual que se realizó con las tasas de mortalidad y de fecundidad y de acuerdo con el patrón pasado y con estas tasas modelo se interpolan matemáticamente las tasas para los diferentes años en los cuales se proyectará la PEA. Este análisis se realiza por género y grupos de edad. Una vez proyectadas las tasas de actividad, se aplican a las proyecciones de población con el fin de estimar la oferta de trabajo para cada grupo de edad y cada género. Para la determinación de las tasas modelo, es importante tomar en cuenta los diferentes factores de orden económico y social, tales como el número y naturaleza de los nuevos empleos que se proyectan hacia el futuro, la evolución en los niveles de instrucción, la magnitud en las pensiones, etc. Para estos análisis se puede recurrir a las experiencias de países desarrollados como un ejemplo para observar la evolución de la PEA. Ejemplo: Un ejemplo hipotético de la aplicación de la técnica se muestra seguidamente. Supóngase que para la población presentada en la sesión anterior, se desea proyectar la demanda de nuevos empleos para los tres quinquenios siguientes al año 2000. Para ello se utilizará como referencia las proyecciones generales de población obtenidas en esa sesión, junto con las tasas de participación o porcentajes de participación en la actividad económica del año 2000. Estas tasas corresponden al grupo constituido por empleados, desempleados y los que buscan trabajo por primera vez, para los grupos quinquenales de edad y sexo. El supuesto básico que se va a utilizar consiste en asumir que las tasas de participación masculina se mantienen constantes, mientras que la participación femenina aumenta a un ritmo del 15% por quinquenio. El siguiente cuadro muestra la población total y la población económicamente activa por sexo y grupos de edad.
Como se indicó anteriormente, los porcentajes de participación de los varones se suponen constantes para los siguientes tres quinquenios, mientras que los valores respectivos de las mujeres se incrementarán en un 15% por quinquenio.
Para la desagregación del grupo de 12 a 14 años se utilizaron los multiplicadores Karup-King desarrollados en la quinta sesión. El análisis hecho señala que para el año 2015, se espera una demanda de 455 963 empleos para ambos sexos, superando en cerca de 180 000 empleos la demanda del año 2000 (272 887). En términos generales, el proceso desarrollado anteriormente puede ser aplicado para proyectar otras demandas o segmentos de la población: población urbano rural, nuevos matrimonios, demanda de aulas o profesores, de viviendas, de camas de hospital, etc. Estimación de población en áreas administrativas menores, uso de los indicadores sintomáticos. Para los años censales se tienen estimaciones de población en áreas administrativas menores de mucha precisión; pero durante el período postcensal, resulta sumamente difícil encontrar cifras de calidad. Debido a la problemática que conllevan estas estimaciones a nivel de áreas administrativas menores, desde hace muchas décadas diversos investigadores han propuesto utilizar los indicadores sintomáticos, como una alternativa razonable al problema. Estos indicadores consisten en variables auxiliares que se encuentran fuertemente correlacionadas con el crecimiento poblacional de una localidad. De este modo, ellas pueden ser utilizadas para medir los cambios que se producen en la población de una localidad. Las variables sintomáticas corresponden a información recolectada regularmente por empresas e instituciones públicas o privadas, para propósitos de orden administrativo; por ejemplo, la matrícula escolar, las declaraciones de impuestos, el número de abonados de los servicios básicos, el número de electores inscritos en el padrón electoral, etc. Es claro, que la intención de recolectar estos datos no consiste en estimar poblaciones, por lo que generalmente se presentan varios problemas con su utilización. Para que una fuente de información pueda considerarse como indicador sintomático de calidad, debe satisfacer cinco condiciones básicas: a) Sensibilidad: El indicador debe presentar una alta correlación con el tamaño poblacional. b) Disponibilidad: Los datos deben estar actualizados periódicamente, mínimo año a año, para cada área menor. c) Confiabilidad: Se debe entender la naturaleza de los datos que se van a utilizar. Es necesario tener claro, ¿dónde y cómo fueron obtenidos?. d) Estabilidad en definiciones de conceptos y en métodos de recolección: La definición de los conceptos y las técnicas de recolección no pueden variar significativamente durante los períodos de interés. e) Facilidad de obtención: Las fuentes de información deben poder ser accesadas fácilmente y en forma oportuna. No deben tener limitaciones de confidencialidad. El incumplimiento de una de estas características, hace muy difícil se aplicación para la estimación de población. Seguidamente se muestran la principales fuentes de información, que pueden ser utilizadas en este tipo de estimaciones. Fuentes de información sintomática: En estudios realizados en Costa Rica para determinar los principales indicadores sintomáticos a nivel nacional, y precisar la calidad de las estimaciones que producían, se consideraron ocho fuentes de información: Padrón electoral: Incluye las personas mayores de 18 años que se encuentran inscritas en el padrón de electores del país de acuerdo con el lugar de residencia que registraron. Esta es una variable que realiza un gran aporte en la estimación de la población adulta. Resulta muy sensible en la medición de la migración interna, pero es completamente insensible ante la migración internacional. Nacimientos y defunciones: Como bien se ha discutido, estas dos variables están fuertemente asociadas con los cambios de población, por esta razón su utilización como indicadores sintomáticos de cambio, da buenos resultados. Estas variables, específicamente los nacimientos, resultan muy sensibles a cierto tipo de la migración internacional. El mayor problema en su utilización radica en problemas con la declaración del lugar de residencia, esto ocurre para la madre, en el caso de los nacimientos, como de los muertos, en el caso de las defunciones. Matrícula en los centros educativos: Representa el número de escolares de enseñanza primaria o secundaria, que se encuentran matriculados en los centros educativos del área administrativa de interés. En países con un alta participación de los jóvenes en los sistemas educativos, esta variable ofrece un gran aporte a las estimaciones de las poblaciones en áreas menores. Aunque se presentan algunos problemas por los desplazamientos de los muchachos hacia otras áreas con la intención de realizar estudios, lo cual si no es sistemático, puede provocar graves errores en las estimaciones. Permisos de construcción de viviendas: Debido a que toda nueva vivienda debe tener un permiso para su construcción, esta es una variable que debería estar fuertemente correlacionada con las magnitudes poblacionales de las áreas administrativas menores. Sin embargo, la experiencia ha demostrado que en los países en desarrollo no siempre se solicitan estos permisos de construcción, fundamentalmente en las áreas administrativas más rurales. Número de asegurados en los servicios de seguridad social: Al igual que en el caso anterior, esta variable es muy diferencial entre países desarrollados y subdesarrollados, y entre las áreas urbanas y rurales; en consecuencia, debe ser utilizada con mucha precaución al momento de introducirla para la estimación de población. Número de abonados a los servicios básicos: El número de abonados a los servicios de electricidad, teléfono, agua, recolección de basura, etc., son variables que se encuentran fuertemente correlacionadas con la magnitud de la población de una área administrativa pequeña. Sin embargo, nuevamente, en países en desarrollo no existe una alta cobertura de muchos de estos servicios, y esta cobertura es muy diferente entre un área administrativa y otra, lo que imposibilita tener una técnica que permita utilizar estas variables en las estimaciones de su población. Existen otras variables como las declaraciones de impuestos municipales, la inscripción de vehículos, la demolición de viviendas, declaraciones de propiedades, etc., que podrían utilizarse para estimar la población de una área administrativa; sin embargo, en la mayoría de países en desarrollo, no proporcionan estimaciones de calidad. En los estudios realizados en Costa Rica, se pudo comprobar que la combinación en el uso del padrón electoral, con los nacimientos y la matrícula escolar en enseñanza primaria, dieron excelentes resultados en las estimaciones de población a nivel provincial, cantonal y distrital. (Chaves, 1997) Las técnicas matemáticas y estadísticas que han sido desarrolladas para estimar la población, por medio del uso de los indicadores sintomáticos, no pretenden realizar estimaciones directas, sino que consisten en estrategias para desagregar una proyección nacional entre las áreas administrativas menores que la constituyen. Estas técnicas se fundamentan en la relación histórica entre el indicador sintomático y la población. Por este motivo, se utiliza la información de uno o dos censos anteriores al momento de efectuar la desagregación de la proyección nacional. Seguidamente se describe brevemente el fundamento teórico de tres de los principales métodos para realizar estas estimaciones. Método de Razón Censal Este método considera las tasas de ocurrencia de un determinado indicador sintomático en cada una de las áreas administrativas. Supone que las áreas locales presentan una razón de cambio proporcional a la del área mayor (que podría ser todo el país), en el período comprendido entre el último censo y el momento en que se realiza la estimación. Supóngase que se desea estimar la población basada en la variable sintomática S para un cantón u, t años después del último censo. Primeramente se calcula: r0(u) es la tasa de ocurrencia del indicador sintomático S para u en el año correspondiente al último censo. S0(u) es la información de la variable sintomática S observado para u en el año correspondiente al último censo. P0(u) es la población del cantón u medida en el último censo. Posteriormente, se busca aproximar la tasa del indicador sintomático al momento t, por medio de un parámetro f, el que representa la razón de cambio en el indicador sintomático entre el año censal y el momento t, tal que: rt(u) = f r0(u) Para estimar el valor de f es necesario tener información del área mayor que contiene a u, para ello se pueden obtener estimaciones independientes de la población en el momento t. Esta área se denota con M y su población en el momento t por Pt (M),. De este modo, se calculan las tasas de ocurrencia de S en el área M, al momento censal 0 y al momento t. Suponiendo que la razón de cambio en el indicador sintomático para el área mayor M puede aproximar efectivamente al valor de f, se tiene: Entonces, la estimación de rt(u) es: Por lo tanto, la estimación poblacional para cada cantón u, en el momento t, viene dada por:
Usualmente se obtiene más de una estimación de Pt(u) utilizando para ello diferentes indicadores sintomáticos. La estimación final es, generalmente, el promedio simple de las estimaciones individuales, aunque se han propuesto métodos para ponderarlas (Ericksen, 1973; Ericksen, 1974). La principal ventaja de este método es la simplicidad de aplicación. Presenta la desventaja que la dirección de las series sintomáticas podría estar afectada por factores distintos a los que justifican el cambio en la población. Esto significa que la razón para un cantón puede cambiar en una proporción diferente y realmente podría, incluso, moverse en dirección contraria a la razón del área mayor; de este modo se incumpliría el supuesto básico del modelo. Método de Diferencia de Tasas Este procedimiento es una variación del método de Razón Censal. La principal diferencia entre los dos métodos radica en la forma de estimar la tasa de ocurrencia del indicador sintomático para cada cantón. El método supone que el crecimiento de esta tasa, para el cantón u, es igual al crecimiento experimentado en ella para el área mayor M. Considerando nuevamente el cálculo de estimaciones por medio del indicador sintomático S, la aproximación para la tasa de ocurrencia de este indicador en el momento t, para el cantón u, viene dada por la fórmula:
donde sus componentes se definen tal y como se especificó anteriormente. Método de Razón Correlación En su forma básica, la aplicación del método consiste en distribuir la población de un área mayor en sus cantones constituyentes. Esta técnica ha demostrado ser uno de los más exactos en la estimación de población poscensal (Namboodiri, 1972; Mandell y Tayman, 1982; Fenney, Hibbs y Guillaspy, 1995). Si el supuesto básico del método asume una relación lineal entre las razones de cambio de las proporciones poblacionales y las razones de cambio de las proporciones de los indicadores, entre dos períodos. Considerando, además, que los cambios en el tiempo en esta relación afectan uniformemente a todos los cantones, se obtiene un modelo más refinado que puede formularse como:
Donde:
para todo cantón u y además ai (i = 0,1) corresponde a los coeficientes del modelo. Los valores P, S, u y M están definidos tal como se indicó en los métodos anteriores y sus subíndices 0 y 1 representan los momentos censales del penúltimo y último censo respectivamente. Esta ecuación indica que la razón de cambio en el tiempo de la proporción poblacional está sistemáticamente relacionada con la correspondiente razón de cambio, en las proporciones de los indicadores. Se pueden introducir al modelo otros indicadores sintomáticos de manera que:
Donde
para cada cantón u y cada indicador sintomático j. Una vez que el modelo de regresión ha sido estimado, resulta muy simple obtener las estimaciones de población para un período poscensal. El Método de Tasa Correlación Se le critica a la técnica Razón Correlación una inconsistencia en su lógica interna, ya que los coeficientes del modelo se obtienen tomando como referencia el tiempo entre los censos y, sin embargo, las estimaciones se efectúan en tiempos diferentes del período base, el cual es, por lo general, menor al tiempo entre los censos. Esto puede afectar la estabilidad natural de los coeficientes y las estimaciones producidas (Mandell y Tayman, 1982; O’Hare, 1980; Swanson, 1980). Se ha propuesto una transformación al método de Razón Correlación, llamada “Tasa Correlación”, que se basa en una aproximación exponencial de cambio, y que se realiza tomando el logaritmo natural de cada razón y dividiéndola entre el tiempo transcurrido entre los censos utilizados como referencia (Swanson y Tedrow, 1984). Formalmente, el modelo se puede expresar por:
donde
:
Yu y Xu,j están definidos tal como se indicó para la técnica de Razón Correlación y k es el intervalo de tiempo transcurrido entre los censos. Anexo sobre la aplicación de las técnicas Sesión
anterior Objetivos
|Importancia|
Proyección del PEA
|Proyección
en áreas menores | |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


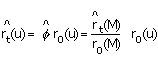
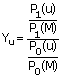 y
y