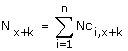Objetivos| Importancia de las proyecciones |Conceptos básicos | Métodos | Método de componentes| Bibliografía | Ejercicios de autoevaluación | Solución de autoevaluación

12. Estimaciones y Proyecciones de población

Bajar para imprimir

Objetivos            

Una vez  finalizado el estudio de la presente sesión, el estudiante será capaz de:  

• Determinar la importancia de contar con estimaciones y proyecciones de población.

• Reconocer los principales problemas en el cálculo y en el uso de estimaciones y proyecciones poblacionales. 

• Definir los  principales conceptos asociados con la teoría de las estimaciones y proyecciones poblacionales.

• Reconocer los fundamentos básicos en la aplicación del método de componentes, método del crecimiento natural y algunos métodos matemáticos.  

• Utilizar los resultados de una tabla de vida para proyectar la mortalidad.

• Utilizar las tasas de fecundidad por grupos de edad para determinar los nacimientos futuros.

• Determinar los principales mecanismos en la proyección de la migración.

• Utilizar las proyecciones de los principales componentes del cambio demográfico en la generación de proyecciones poblacionales.

¿Cuál es la necesidad de estimar o proyectar la población?

La movilidad espacial de los habitantes de una localidad, región o país, provoca una redistribución geográfica de la población.  Como se ha repetido a lo largo del curso, los cambios en la mortalidad y la natalidad, junto con los movimientos migratorios,  facilitan los constantes cambios en el tamaño y la distribución de la población.  La combinación de estos elementos dificulta la tarea de estimar el tamaño y composición de la población de una localidad en un momento dado. 

La necesidad de contar con estimaciones y proyecciones de población radica en su importancia para la planificación de diferentes actividades, tanto a nivel gubernamental como de empresa privada.  En efecto, numerosas instituciones públicas o privadas destinadas a brindar servicios como:  educación, salud, infraestructura vial, seguridad social, comercio, etc., requieren de estas cifras para planificar las demandas y necesidades de los usuarios.  Por otro lado, actualmente, la planificación a nivel regional ha ganado gran importancia con respecto a la estrategia general de los planes de desarrollo de un gobierno central.  Esto obliga a los gobiernos municipales, a conocer las principales características socio-demográficas de las distintas localidades y sus necesidades básicas para el futuro.  

¿Qué tipo de proyecciones poblacionales se deben realizar?

Las estimaciones y proyecciones de población pueden efectuarse a nivel nacional o estar referidas a diferentes tipos de áreas político-administrativas:  provincias, departamentos, estados, cantones, distritos, etc.  Sin embargo, desde el punto de vista de la planificación central de la economía de una nación, pueden ser más necesarias proyecciones de población dirigidas a otras unidades territoriales, entre ellas las proyecciones regionales.  Esta regionalización que se realiza en la mayoría de países, responde a intereses meramente de la planificación y no necesariamente al orden político-administrativo.  Otra clasificación de gran relevancia para la planificación de la economía de un país, consiste en la urbano-rural.  Esta clasificación es la que más destaca las diferencias económicas, sociales y demográficas de su población.

Sin embargo, se pueden determinar otros tipos de proyecciones y estimaciones, dirigidos a sectores particulares, tales como:  población económicamente activa (PEA),  población en edad escolar, población de mujeres en edad fértil, población mayor a los 65 años, etc.

¿Cuáles son los principales problemas que acarrea la generación de las proyecciones de población?

Las proyecciones nacionales de población son las que presentan los menores problemas, sin embargo, en algunas ocasiones, los fuertes movimientos migratorios pueden provocar que se incurra en graves errores a este nivel.  No obstante, los mayores problemas se presentan al proyectar o estimar la población en diferentes subdivisiones administrativas o regionales, así como en grupos particulares de la población.  

En las subdivisiones administrativas y en grupos particulares de la población, el componente migratorio juega especial importancia, pues muchas veces su impacto supera al que se presenta por medio del crecimiento vegetativo.  Además, por las características de este componente, resulta sumamente difícil predecir su comportamiento futuro.  Otro problema básico, radica en la calidad y disponibilidad de datos demográficos para las diferentes áreas de interés.  Aunque, la calidad de la información vital general de una país sea la óptima, generalmente a nivel de áreas administrativas, la precisión nos es la misma ya que se tienden a presentar problemas en las declaraciones del lugar de residencia, edad, etc.  Además, si se trabaja en áreas administrativas menores, los problemas se incrementan pues existe mucha inestabilidad en la magnitud de los datos entre un año y otro.

Terminología básica

A continuación se definen algunos de los principales términos que se han utilizado y que se emplearán a lo largo de este capítulo. 

Estimación demográfica:  Indicador o valor calculado de un parámetro relativo a una variable específica de la población (Rincón, 1990).

Estimación de población: Es el número de personas que se calcula tiene o tuvo una población en un momento específico del tiempo, ya sea globalmente o de una categoría más reducida.  Tal volumen no es el producto de medición directa, pero para obtenerla, se tuvo en cuenta alguna información sobre la población (Rincón, 1990).

Proyección de población : Es en definitiva el resultado de un conjunto de estimaciones demográficas, matemáticas o de otro tipo, por medio de las cuales se busca establecer las tendencias más plausibles de las variables determinantes de la dinámica poblacional y, con ello, la derivación de los volúmenes de población y de sus principales características hacia el futuro.  (Rincón, 1990).

Proyecciones de corto plazo:  Partiendo de una población base o población inicial, se hace referencia a aquellas proyecciones que se realizan para los cinco años posteriores.

Proyecciones de mediano plazo:  En este caso se refiere a las proyecciones que se realizan para periodos que van de los cinco años hasta los veinte años siguientes con respecto a la población base.

Proyecciones de largo plazo:  Se refiere a las proyecciones que se realizan para periodos más allá de los veinte años, posteriores a la población de referencia inicial o población base.

Retroproyecciones:  En este caso se hace referencia a las estimaciones que se realizan hacia el pasado.  Al igual que en los casos anteriores, se parte de una población base y se busca predecir la población de los años anteriores. 

Modelos agregativos de estimación poblacional:   Consiste en aquellos métodos que realizan estimaciones independientemente para cada área geográfica particular, que obtienen las proyecciones nacionales por suma de éstas (Rincón, 1989)

 Modelos desagregativos de estimación poblacional:  Consisten en aquellas técnicas de estimación, que a partir de las estimaciones nacionales se lleva a cabo una desagregación de ellas, para obtener las estimaciones regionales y para áreas menores (Rincón, 1989).

 Estimaciones individuales:  Se refieren a aquellas que se hacen para una o algunas localidades, pero sin que sus resultados estén afectados por el valor estimado de los demás, o sea, que la suma de las estimaciones de las sub áreas no tiene que reproducir el total de la población del área mayor, que ha sido o no, estimada en forma separada (Granados, 1988).

 Estimaciones en conjunto:  Son aquellas que se hacen para un grupo de sub áreas y por lo tanto, los resultados finales dependen de las estimaciones de todas las localidades (Granados, 1988).

Proyecciones derivadas: Corresponden a estimaciones que se realizan sobre una proyección con respecto a  ciertas necesidades de la población por ejemplo:  necesidades futuras de maestros, médicos, camas hospitalarias, policías, etc.

¿Cuáles son los principales métodos para efectuar estimaciones y proyecciones de población?

A continuación se mencionan algunas de las técnicas que se utilizan para estimar la población de una localidad.  En realidad existen muchas otras técnicas; sin embargo, no se pretende ser exhaustivo en este sentido, sino simplemente conocer algunos de los mecanismos que tradicionalmente han sido utilizados para realizar esta labor. 

El método de los componentes:  Desde hace muchos años, el “método de los componentes” se ha conocido como el modelo básico para elaborar estimaciones demográficas.  Su principio básico consiste en desagregar el crecimiento de la población  en sus componentes demográficos fundamentales por medio de la ecuación compensadora. 

N _{x + k}  =  N_x + B_{x + k} - D_{x + k} + SM_{x + k}

 donde:  N_{x + k}  es la población estimada k años después del año base x

             N_x  es la población en el año base x

             B_{x + k}  es el número de nacimientos ocurridos entre el año x y el año x + k

             D_{x + k}  es el número de defunciones ocurridas entre el año x y el año x + k

             SM_{x + k}  es el saldo migratorio que tuvo lugar entre el año x y el año x + k

Un segundo aspecto importante dentro de este método, es que puede ser aplicado a sub poblaciones o cohortes de personas con una o más características: sexo, edad, grupos étnicos, etc.  Cuando se utiliza el método de esta forma, la población total viene dada por:

donde: Nc_{i, x + k}  corresponde a la población de la cohorte i en tiempo x + k  y  

Nc_{i, x + k} = Nc_i,x + Bc_{i,x + k} - Dc_{i,x + k} + SMc_{i,x + k}   

Los términos están definidos igual que antes, salvo por la especificación de la cohorte dada c_i.  Una adecuada aplicación del método de los componentes, requiere precisión de los datos correspondientes a sus componentes demográficos.  Si alguno de ellos fuera desconocido se hace necesario llevar a cabo un diagnóstico de la dinámica de dicho componente en la región en consideración, y con base en esto postular hipótesis respecto al cambio esperado para el periodo poscensal.

El método del crecimiento natural:  Este es un caso particular del método de componentes, y consiste en suponer crecimiento natural, lo cual quiere decir que se considera que el saldo migratorio es nulo, para cada una de las áreas, con lo cual el tamaño de la población al momento t viene dado por la ecuación:

N_{x + k}  =  N_x + B _{x + k} - D _{x + k}

Donde los términos están definidos igual que antes.  Obviamente este método produce serios errores, fundamentalmente en aquellas poblaciones con fuertes movimientos migratorios internos y externos.

Los modelos matemáticos:  Otra posibilidad para efectuar estimaciones poblacionales a nivel de área menor, consiste en suponer  que el crecimiento de la población en las dichas áreas, presenta un comportamiento regular  y que las condiciones que lo afectan se mantendrán constantes en el futuro o variarán en forma gradual.  Por lo que se permite utilizar ciertos modelos matemáticos, los que utilizan las tasas anuales de crecimiento poblacional, obtenidas en el periodo intercensal anterior, de acuerdo con los supuestos sobre el tipo de crecimiento que experimenta el área en consideración.  Estos modelos fueron analizados en el capítulo 5, corresponden a  tres funciones matemáticas que permiten estimar y proyectar la población:

                   N_x+t =  N_x  (1 + k r),  el modelo supone un crecimiento lineal o aritmético.

                   N_x+t =  N_x  (1 + r) ^k,   el modelo supone un crecimiento geométrico.

                   N_x+t =  N_x   e ^{r k},   el modelo supone un crecimiento exponencial. 

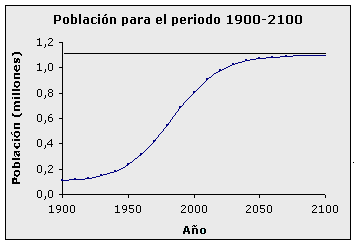
Donde  P_x+k y  P_x se definen igual que antes, r representa la tasa de crecimiento poblacional anual para el área en mención.  Dentro de estos modelos, el primero es el más conservador, mientras que el tercero proporciona las estimaciones, más elevadas.

Muchos otros modelos matemáticos han sido utilizados para proyectar una población, uno de ellos, que ha tenido buenos resultados a nivel general, corresponde al modelo logístico.  La representación gráfica de esta función toma la forma de una S alargada, con dos asíntotas, una inferior y la otra superior.  Supone que inicialmente la población crece a un ritmo lento, pero posteriormente se acelera el crecimiento de una manera brusca y por último se reduce con la misma intensidad con que se inició.  De esta manera se supone que la población se va estabilizando tendiendo a un valor asintótico k.  

El valor asintótico de 1,1 millones representa el valor a que se espera se estabilice esta población alrededor del año 2080.  La fórmula matemática de esta función es:

 donde:   N_x  es la población en el año x

             k corresponde a la asíntota superior de la curva

             a y b son constantes que se deben estimar

Se han hecho muchas modificaciones a este modelo; sin embargo, los resultados no han ofrecido sustantivas mejoras con respecto al modelo original.

Proyección de los componentes

El nombre de este método se debe a que su estrategia metodológica consiste en proyectar los tres componentes del cambio poblacional:  mortalidad, natalidad y migración.  Seguidamente se presenta una descripción básica sobre la aplicación de esta técnica.

El primer paso requiere hacer un análisis detallado del comportamiento pasado de cada uno de los componentes, con la finalidad de tratar de establecer tendencias sobre el comportamiento esperado para el futuro.

En segundo lugar, se debe establecer una población base distribuida por sexo y grupos de edad.  Generalmente se toma el último censo de población como referencia y se realizan las correcciones de los diferentes errores que pudiera contener el censo:  cobertura, declaraciones de edad y lugar de residencia, etc., que pudiera haber presentado este censo.  También se hace necesario, trasladar las población del censo y su distribución por sexo y edad al 30 de junio del año que se quiere utilizar como referencia.  Si se desean realizar proyecciones quinquenales, entonces es conveniente efectuar este traslado hasta un año terminado en cero o en cinco. 

Como última etapa, a partir de la población base se proyecta cada grupo de edad hacia el nuevo período (generalmente 5 años) de acuerdo con las tendencias esperadas en los patrones de fecundidad, mortalidad y migración.  El proceso se repite tantas veces como sea necesario para alcanzar el año hasta el cual se pretende proyectar esta población.

Proyección de la mortalidad:  Primeramente se estiman las tasas específicas de mortalidad (_nm_x), por sexo y grupos de edad (grupos quinquenales), para los años anteriores.  Estas tasas pueden ser determinadas por medio de las estadísticas vitales o por medio de métodos indirectos, para aquellos casos en que no se cuenta con información vital de calidad.  De acuerdo con su evolución pasada y analizando las perspectivas futuras en mortalidad, se proyecta el patrón de comportamiento futuro de estas tasas, considerando que pueden llegar a estabilizarse en determinado momento.  Con esta información, se estima el comportamiento de las tablas de vida para el futuro y específicamente se determinan las relaciones de supervivencia (_nP_x,x+n-1),por sexo y grupos de edad, para cada uno de los períodos en que se van a realizar las proyecciones.  Son precisamente estas relaciones de supervivencia las que permiten proyectar cada grupo n años hacia el futuro, suponiendo que no existe migración.

Proyección de la fecundidad:  Al igual que se realizó con la mortalidad, se requiere estimar el comportamiento pasado de las tasas específicas de fecundidad y de la tasa global de fecundidad.  Nuevamente estas estimaciones pueden llevarse a cabo por medio de las estadísticas vitales o de métodos indirectos.  Con esto se pretende proyectar estas tasas hacia el futuro, específicamente para el período de interés.  Del mismo modo que se realizó con la mortalidad, se supone que la tasa global de fecundidad debe llegar a estabilizarse en cierto momento.  En este caso se espera que alcance el nivel de reemplazo (TGF = 2,1) para cierto año determinado, y las tasas específicas se proyectan hacia ese valor.  En este sentido generalmente se consideran tres supuestos básicos:

Hipótesis baja:  La fecundidad alcanza el nivel de reemplazo dentro de un período de tiempo relativamente corto. En este caso se espera un decrecimiento de la fecundidad más fuerte de los esperado.

Hipótesis media o esperada:  Supone que la fecundidad alcanza el nivel de reemplazo siguiendo el patrón de descenso que se ha experimentado en los años anteriores.

Hipótesis alta:  Supone que la fecundidad alcanza el nivel de reemplazo en un término mayor del esperado, lo cual indica que el ritmo de descenso en la fecundidad, disminuye para el período en que se pretende proyectar la población. 

Esta tasas proyectadas permiten estimar los nacimientos que se esperaría ocurrieran en cada período.

Proyección de la migración:  Indudablemente el componente migratorio es el más complejo para predecir su comportamiento venidero.  No basta con efectuar una análisis retrospectivo para poder analizar lo que podría pasar en el futuro.  Se requiere además, de todo un estudio sobre diferentes elementos tales como:  la economía, la situación política, situación laboral, climatológica, etc., pero no solo de la localidad para la cual se está proyectando la población, sino para las localidades vecinas.  Aun con estudios, de este tipo resulta sumamente difícil poder aproximar lo que se espera de este componente a mediano o largo plazo.  Por esta razón, muchas veces se proyecta la población suponiendo únicamente una migración constante o decreciente en su magnitud, utilizando como referencia lo que se ha presentado en el pasado.  También es posible, suponer que no se presentará migración futura. 

Aplicación del método:  Suponga que se desea estimar una población en grupos quinquenales de edad en períodos de 5 años.  La proyección para los grupos intermedios de edades para el año t + 5, tomando como referencia el año t, viene dada por:

donde:

Un análisis diferente debe ser utilizado para los grupos de edad primero y último.  En el caso del último grupo, bajo el supuesto de que corresponde a 85 años y más, la proyección de este grupo se obtiene por medio de la ecuación:

Finalmente, para proyectar el grupo de edad de 0 a 5 años, se requiere estimar el número de nacimientos que se producirían entre los años t y t +5, para ello es necesario hacer uso de las tasas de fecundidad para este período.  De este modo, los nacimientos producidos en el período vienen dados por:

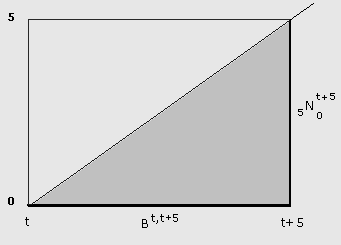
Además como las tasas son anuales, en la fórmula aparece el factor 5 que muestra la cantidad de nacimientos para los 5 años.  Esta fórmula proporciona los nacimientos totales; sin embargo, se puede utilizar el valor del índice de masculinidad (105 niños por cada 100 niñas) para estimar los nacimientos por sexo.  Esta población media puede ser estimada simplemente por el promedio de la población femenina de los años t y t+5, por lo que la estimación de los nacimientos viene dada por:

Entonces la proyección de la población del primer grupo se obtiene por:

Gráficamente se puede mostrar esta proyección mediante un diagrama de Lexis:

Con la ayuda de una hoja electrónica de cálculo, se puede simplificar la aplicación del procedimiento.  

Ejemplo en la aplicación de la técnica:  Considere una población hipotética al 30 de junio del año 2000, la cual se desea proyectar por quinquenio hasta el año 2015.  Se supone que la población para el 2000 ya está corregida.  

En primer lugar para proyectar la mortalidad para los siguientes 15 años se requiere construir tablas de mortalidad por sexo, para cada uno de los quinquenios considerados: 2000-2005, 2005-2010 y 2010-2015. Es este caso se puede estimar que las tasas de mortalidad se estabilizan a partir del quinquenio 2005-2010, por lo que se necesitan únicamente las tablas de los dos primeros quinquenios, suponiendo que esta última se puede tomar como el patrón más bajo que se puede alcanzar.  Este supuesto obliga que las tasas específicas de mortalidad por sexo, desciendan paulatinamente hasta que alcancen este valor límite.  Esta proyección se puede realizar utilizando modelos matemáticos simples:  interpolación lineal o exponencial, o cualquier otra técnica de aproximación.  

El siguiente cuadro muestra las tasas específicas de mortalidad para el año 2000 corregidas y las tasas esperadas para el año 2010:

Seguidamente se procede a proyectar las tasas específicas de fecundidad.  En este caso se supone que el nivel de reemplazo se alcanzará en el año 2013.  Las tasas observadas para el año 2000 y esperadas para el 2013, se presentan en el siguiente cuadro:

Nuevamente mediante interpolaciones matemáticas, se pueden estimar las tasas específicas de fecundidad para los años 2003 y 2008, que van a corresponder a los períodos 2000-2005 y 2005-2010 respectivamente.  El siguiente cuadro muestra los resultados de estas interpolaciones.

Finalmente, se debe considerar el componente migratorio; de acuerdo con la información de el último censo y con la ayuda de otras técnicas indirectas se pudo estimar que durante el período 1995-2000 el saldo migratorio fue positivo y correspondió a  15 417 varones y 11 568 mujeres.  La distribución por grupos de edad y sexo se presenta en el siguiente cuadro:   

Con respecto a estos saldos migratorios, se pueden considerar varias hipótesis, la primera consiste en suponer que para los próximos años el saldo va a ser nulo; sin embargo, no parece razonable de acuerdo con lo experimentado recientemente.  Una segunda hipótesis consiste en mantener constantes los flujos migratorios.  Finalmente puede suponerse que la migración va a disminuir proporcionalmente, por lo que se puede recurrir a señalar un porcentaje fijo de disminución por quinquenio.  En este ejemplo hipotético, se supondrá que los saldos migratorios descienden un 20% por quinquenio.  El cuadro siguiente muestra los resultados de la aplicación de dicha hipótesis.

Con toda la información anterior se procede a efectuar la proyección de población.  Como primer paso se proyectan los grupos de edad de 5 años y más, utilizando las relaciones de sobreviviencia y el saldo migratorio.  Por medio de una hoja electrónica se pueden realizar los cálculos de una manera muy simple.  A continuación se presenta la proyección de la población femenina para el año 2005.

    ¹Corresponde a la relación de sobrevivencia de 80 años y más. 

Para estimar los nacimientos se recurre a las tasas proyectadas de fecundidad para el quinquenio, tal como se detalla seguidamente.

Finalmente la proyección de población para el primer grupo de edad correspondiente al año 2005, por sexo, viene dada por:

Utilizando los mismos procedimientos, se generan las proyecciones para los otros quinquenios.  El siguiente cuadro resume la proyección completa.

Tarea de la sesión

Sesión anterior | siguiente

Inicio de la página

Objetivos| Importancia de las proyecciones |Conceptos básicos | Métodos | Método de componentes|
Bibliografía | Ejercicios de autoevaluación | Solución de autoevaluación