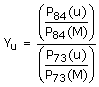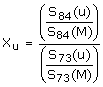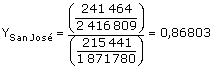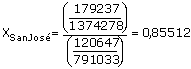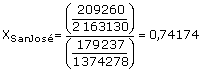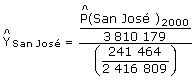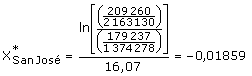Anexos sesión 13

Bajar para imprimir

Ejemplos de aplicación de los métodos

Para que el lector pueda tener una mejor comprensión en la aplicación de las técnicas de estimación poblacional, este anexo presenta un ejemplo de cálculo.  Se efectuaron estimaciones de la población del cantón Central de San José, utilizando en cada caso la información del padrón electoral.

 Método de Razón Censal:  Para analizar un ejemplo de esta técnica, se debe contar con la tasa de electores para cada cantón y para Costa Rica en 1973.  Además, un estimado de la tasa de electores para Costa Rica en 1984.  De acuerdo con la información proporcionada por el Cuadro A 1.3 del Anexo 1, para el cantón Central de San José se tiene:

Entonces, si se representa con r  la tasa de electores inscritos, se tiene que:

 La técnica supone que la tasa de electores de San José para el 2000, viene dada por: 

r (San José)₂₀₀₀  = f r (San José) ₁₉₈₄

donde el valor de f, puede ser estimado por:  

Con lo cual, la estimación de r(San José)₂₀₀₀ es:  

 La estimación simple de la población para el cantón central de San José en el 2000 viene dada por:                                                  

Este proceso se efectuó para los 81 cantones, por lo que la suma de las estimaciones poblacionales de todos ellos debe coincidir con la población total del país (3 810 179).  Sin embargo, la suma de las estimaciones simples para todos los cantones es 3 879 263.  Por esta razón es necesario prorratear las estimaciones, de manera que la suma de ellas coincida con la población censal de Costa Rica para 2000.  Para este fin, la estimación de cada cantón se multiplica por el cociente:

Por lo tanto, la estimación  de la población de San José, al 30 de junio del 2000 (fecha del censo), viene dada por:

 Entonces el error porcentual para la estimación anterior es:

 Se puede decir que el método de Razón Censal produjo una subestimación de un 10,4% con respecto a su valor censal de la población de San José.

 Método de Diferencia de Tasas:  Este método es una variante del procedimiento de Razón Censal.  La única modificación radica en la forma de estimar la tasa de ocurrencia del indicador sintomático.  En el ejemplo anterior se obtuvieron los valores  r(San José)₁₉₈₄ = 0,74229, r(Costa Rica)₁₉₈₄ = 0,56863 y r(Costa Rica)₂₀₀₀ =  0,56772

Por medio del procedimiento Tasa Correlación se supone que la tasa de electores de San José, para 1984, viene dada por:

r (San José)₂₀₀₀  = r(San José) ₁₉₈₄ + [ r(Costa Rica)₂₀₀₀ - r(Costa Rica)₂₀₀₀ ]

 Con lo cual, según esta técnica la estimación de r(San José)₂₀₀₀ es:

Así, la estimación simple de la población para 1984 está dada por: 

Para este caso, la suma de las estimaciones simples para todos los cantones es 3 873 405 y la estimación de la población de San José es:

 El error porcentual asociado es :

Por lo que se concluye que la estimación poblacional subestimó el valor censal en 10,3%.

Método de Razón Correlación:  Para la aplicación de este método se requiere información de dos censos anteriores al momento de la estimación: 

La técnica utiliza el modelo de regresión lineal:

donde a_i  (i =  0,1)  corresponde a los coeficientes obtenidos por mínimos cuadrados,   y para este caso:          

para todo cantón u. 

P(u) es la población censal correspondiente al cantón u

P(M) es la población censal de Costa Rica

S (u) es el número de electores inscritos en el padrón electoral para el cantón u

S (M) es el número de electores inscritos en el padrón electoral para Costa Rica

De este modo, Y_u y X_u representan las razones de cambio de las proporciones que representa cada cantón del total del país, para el período 73-84.  Para San José, estas razones están dadas por:

Una vez determinadas las razones de cambio en el período 73-84 para los 81 cantones, se procede a utilizar mínimos cuadrados para obtener los coeficientes del modelo.  El siguiente cuadro presenta los resultados dados por el paquete estadístico SPSS:

La prueba “F” indica que el modelo es altamente significativo.  El valor de R² = 0,80, muestra que el 80% de la variación de la razón de cambio en la proporción poblacional es explicada por la variación de la razón de cambio en la proporción del número de electores inscritos. 

El modelo de regresión lineal estimado viene dado por:

La razón de cambio en la proporción poblacional para San José, en el período  1984-2000, se estima por:

Como para el período 1984-2000 la razón de cambio en la proporción del padrón es:

entonces el valor estimado para la razón de cambio en la proporción de la población sería:

Para el período 1984-2000 se tiene que:

Con lo que se tiene que:

Entonces,  la estimación simple para la población de San José al 30 de junio del 2000 (fecha del censo), viene dada por :

No obstante, la suma de las estimaciones poblacionales para los 68 cantones  es 2434460, que no reproduce la población total de Costa Rica (2416809).  Por esta razón, es necesario prorratear las estimaciones simples obtenidas, por lo que la estimación poblacional para San José es:

Debido a que el valor censal de la población de San José fue 309 672, el error porcentual de la estimación es:

Lo cual quiere decir, que la estimación realizada por este método subestimó en un 2,4% la población censal de San José.

Método de Tasa Correlación:  En la aplicación del método de Tasa Correlación se mantienen los principios básicos utilizados por el Método de Razón Correlación.   La principal diferencia entre los dos métodos es la forma en que se aplica la razón de cambio en las proporciones.  Formalmente el modelo se puede expresar por:

donde :              

Y_u y X_u   están definidos tal y como se indicó para la técnica de Razón Correlación y k corresponde al intervalo de tiempo transcurrido entre los censos.

De acuerdo con los cálculos hechos anteriormente, para San José, en el período 73-84, Y_{San José} = 0,86803 y X_{San José} = 0,85512.  Además k = 11,06 y representa el tiempo transcurrido entre los censos del 73 y 84 en años.  Entonces:

Después de calculados estos valores en el período 73-84 para los demás cantones, se utilizan de nuevo mínimos cuadrados para obtener los coeficientes a₀ y a₁.  El siguiente cuadro presenta los resultados obtenidos por medio del paquete estadístico SPSS, respecto a la aplicación de dicho método.

Nuevamente la prueba “F” muestra que el modelo es altamente significativo.  El valor de  R² = 0,83, indica que el 83% de la variación de Y_u^* es aclarada por medio de la variación en X_u^*.  Puede notarse que el porcentaje de explicación de este modelo es ligeramente superior al modelo anterior.

 El modelo de regresión lineal estimado es:

 Entonces para el cantón Central de San José, la estimación viene dada por:

Para el período intercensal 1984-2000, el tiempo transcurrido es  k = 16,07, entonces: 

con lo cual:

Entonces

 Por lo tanto, la estimación simple para la población de San José viene dada por :

La suma de las estimaciones poblacionales para los 81 cantones es 3 803 412.  Por lo tanto, la estimación poblacional para San José es:

 El error porcentual en la estimación es:

Lo que da una subestimación del valor censal de un 4,3%.

Las cuatro estimaciones realizadas utilizan un único indicador sintomático, pero la experiencia indica que las mejores estimaciones se producen cuando se combinan más de un indicador.  El siguiente cuadro muestra un análisis de los errores que se produjeron al utilizar estas técnicas para estimar los cantones de Costa Rica en los últimos dos años censales. 

Nota: todo el análisis se hizo con el valor absoluto de errores porcentuales.

Fuentes: Chaves, Edwin  (1997).  Indicadores sintomáticos en las estimaciones poblacionales para áreas menores. Costa Rica.  Tesis para optar al grado de Magister Scientiae, Universidad de Costa Rica.  San José, Costa Rica.

Chaves, Edwin.  Validación de los indicadores sintomáticos en las estimaciones poblacionales:  Censo del 2000.  Jornadas de Análisis Estadístico.  Escuela de Estadística, UCR.  2002.

Puede notarse como la combinación de los indicadores:  padrón electoral, nacimientos y matrícula escolar reducen los errores en las estimaciones de población. 

Volver a sesión 13
Sesión anterior

Inicio de la página