|
|
Práctica 4:
Correlación y Regresión
 Bajar para imprimir Bajar para imprimir
4.1 El gerente de mercado
de una industria de detergentes piensa que las ventas anuales dependen de la
cantidad que invierta en publicidad. El gerente general no está de acuerdo
con él y a perdido datos. A continuación se presentan los datos
correspondientes a seis años
|
AÑO
|
MILLONES GASTADOS
EN PUBLICIDAD
|
MILLONES DE VENTAS
ANUALES
|
|
|
|
|
|
1987
|
2
|
20
|
|
1988
|
3
|
25
|
|
1989
|
5
|
34
|
|
1990
|
4
|
30
|
|
1991
|
11
|
30
|
|
1992
|
5
|
31
|
|
|
|
|
a)
¿Qué porcentaje de la variabilidad de las ventas se explica por su relación
lineal con los montos destinados a la publicidad? R/ 0,2553
b)
El gerente del mercadeo desea determinar una ecuación lineal, para predecir
las ventas anuales a partir de las cantidades destinadas a la publicidad. R/
y = 24,33 + 0,8x
|
4.2
|
En la contabilidad de costos con frecuencia se trata de estimar los
gastos indirectos basándose en el número de unidades producidas. La gerencia
de una empresa ha reunido información sobre esos gastos y las unidades
producidas en diferentes plantas, con el fin de estimar una ecuación de
regresión que le permita predecir los gastos indirectos.
A continuación se presenta esta información:
|
|
Gastos indirectos
|
191
|
170
|
272
|
155
|
280
|
173
|
234
|
116
|
153
|
178
|
|
Unidades
|
40
|
42
|
53
|
35
|
56
|
39
|
48
|
30
|
37
|
40
|
|
a)
|
Determine el coeficiente de correlación e interprételo R/ 0,9835
|
|
b)
|
Calcule la ecuación de regresión R/ y = -80,44 + 6,49x
|
|
c)
|
Prediga el gasto indirecto cuando se producen 50 unidades. R/ 244,1
|
|
d)
|
Determine el error estándar de estimación R/ 10,2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3
|
Los corredores de bienes raíces a menudo quieren saber como el avalúo
de una casa cambia según el tamaño de la misma. Debido a la devaluación, los
datos de avalúo se tradujeron a dólares. A continuación se incluyen algunos
datos sobre la superficie (en cienes de metros
cuadrados) y sobre el avalúo (en miles de dólares) de una muestra de 11
casas.
|
|
AREA
|
1,0
|
1.4
|
1,5
|
1,5
|
1,3
|
1,2
|
1,0
|
1,6
|
1,8
|
1,4
|
1,2
|
|
VALOR
|
40
|
49
|
54
|
51
|
48
|
46
|
41
|
56
|
62
|
50
|
45
|
|
a)
|
Estime la ecuación de regresión (mínimos cuadrados) para predecir el
avalúo a partir del tamaño de la casa R/ y = 14,17 + 25,91 x
|
|
b)
|
Interprete, en términos de problema, el coeficiente de regresión
|
|
c)
|
Calcule e interprete la bondad de ajuste. R/0,9751
|
|
d)
|
Pruebe H0: β = 0 vrs H1:
β>0 con α = 5% R/ Se
rechaza H0
|
|
e)
|
¿Qué valor se espera para una casa de 140 metros cuadrados? R/ $ 50
450,68
|
|
4.4
|
Al aplicar el módulo de “REGRESIÓN” del paquete de cómputo EXCEL a los
datos del ejercicio 4.3 se obtuvo los siguientes resultados:
|
|
Estadísticas de la regresión
|
|
|
|
|
Coeficiente de correlación múltiple
|
0,987483666
|
|
|
|
|
Coeficiente de determinación R^2
|
0,975123991
|
|
|
|
|
R^2 ajustado
|
0,97235999
|
|
|
|
|
Error típico
|
1,075106951
|
|
|
|
|
Observaciones
|
11
|
|
|
|
|
|
|
|
|
|
|
ANÁLISIS DE VARIANZA
|
|
|
|
|
|
|
Grados de libertad
|
Suma de cuadrados
|
Promedio de los cuadrados
|
F
|
|
Regresión
|
1
|
407,7791236
|
407,7791236
|
352,794372
|
|
Residuos
|
9
|
10,40269461
|
1,155854957
|
|
|
Total
|
10
|
418,1818182
|
|
|
|
|
|
|
|
|
|
|
Coeficientes
|
Error típico
|
Estadístico t
|
Probabilidad
|
|
Intercepción
|
14,17215569
|
1,896665233
|
7,472143974
|
3,8024E-05
|
|
area
|
25,91317365
|
1,379620952
|
18,78282119
|
1,5786E-08
|
Compárelos
con sus respuestas e interprételos
|
4.5
|
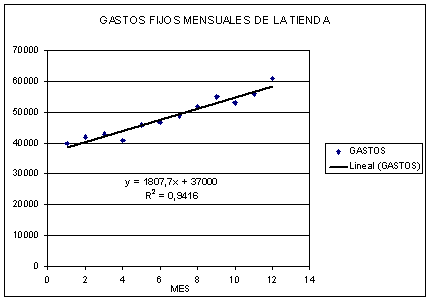
A continuación se presentan los gastos fijos mensuales (en colones)
realizados por una tienda durante los últimos 12 meses.
|
|
MES
|
GASTOS
|
MES
|
GASTOS
|
MES
|
GASTOS
|
|
1
|
40000
|
5
|
46000
|
9
|
55000
|
|
2
|
42000
|
6
|
47000
|
10
|
53000
|
|
3
|
43000
|
7
|
49000
|
11
|
56000
|
|
4
|
41000
|
8
|
52000
|
12
|
61000
|
|
a)
|
Establezca un modelo de regresión lineal simple con los datos
anteriores.
R/ y = 37000 +1807,69x
|
|
b)
|
Dibuje en el diagrama de dispersión, la recta de regresión.
|
|
c)
|
Calcule e interprete el coeficiente de determinación. R/ 0,9416
|
4.6 Al realizar un
diagrama de dispersión con el Excel a los datos del ejercicio 4.5 se obtuvo
lo siguiente:
Compárelos
con sus respuestas e interprételos.
|
4.7
|
Un consultor quiere averiguar la exactitud con que nuevo índice de
rendimiento en el trabajo mide lo que es importante para una corporación.
Una manera de verificar consiste en examinar la relación entre dicho índice
y el salario del empleado.
Se seleccionó una muestra de 8 empleados y se reunió información sobre
el salario (en miles) y el índice (1-10; donde 10 es óptimo).
|
|
Indice del
desempeño
en el trabajo (x)
|
9
|
7
|
8
|
4
|
7
|
5
|
5
|
6
|
|
Salario (¢ miles por semana) (y)
|
36
|
25
|
33
|
15
|
28
|
19
|
20
|
22
|
|
a)
|
Calcule la ecuación de regresión R/ y = -2,11 + 4,21x
|
|
b)
|
Determine el error estándar de estimación R/ 1,3316
|
|
c)
|
Calcule un intervalo de confianza para el salario promedio de los
trabajadores con un índice de 7,5. Utilice α = 0,05 R/ (28,07; 30,91)
|
|
d)
|
Calcule un intervalo de confianza para el salario de un trabajador con
un índice de 5,8. Utilice α = 0,05. R/ (18,7; 25,8)
|
|
|
|
4.8
|
Con el fin de determinar la asociación entre el nivel de ventas, el
precio y la publicidad de cierto producto, se estudió la información
correspondiente a 12 semanas obteniéndose los siguientes resultados:
|
|
VENTAS
|
PUBLICIDAD
|
PRECIO
|
|
1000
|
100
|
20
|
|
1200
|
200
|
22
|
|
1200
|
230
|
23
|
|
1400
|
250
|
25
|
|
1400
|
280
|
25
|
|
1300
|
270
|
24
|
|
2000
|
500
|
32
|
|
2000
|
600
|
32
|
|
1800
|
480
|
30
|
|
2000
|
500
|
34
|
|
2500
|
600
|
34
|
|
2600
|
700
|
36
|
|
|
|
|
|
Calcule e interprete el coeficiente de correlación parcial de:
|
|
a)
|
Las ventas con la publicidad eliminando el efecto del precio R/ 0,45
|
|
b)
|
Las ventas con el precio eliminando el efecto de la publicidad. R/ 0,44
|
|
4.9
|
Al aplicar el módulo de “REGRESIÓN” del paquete de cómputo EXCEL a los
datos del ejercicio 5.9 se obtuvo los siguientes resultados:
|
|
Estadísticas
de la regresión
|
|
|
|
|
|
Coeficiente
de correlación múltiple
|
0,97710074
|
|
|
|
|
|
Coeficiente
de determinación R^2
|
0,954725856
|
|
|
|
|
|
R^2 ajustado
|
0,944664935
|
|
|
|
|
|
Error típico
|
124,0693719
|
|
|
|
|
|
Observaciones
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
ANÁLISIS DE
VARIANZA
|
|
|
|
|
|
|
|
Grados de
libertad
|
Suma de
cuadrados
|
Promedio de
los cuadrados
|
F
|
|
|
Regresión
|
2
|
2921461,119
|
1460730,559
|
94,8944795
|
|
|
Residuos
|
9
|
138538,8813
|
15393,20904
|
|
|
|
Total
|
11
|
3060000
|
|
|
|
|
|
|
|
|
|
|
|
|
Coeficientes
|
Error típico
|
Estadístico t
|
Probabilidad
|
|
|
Intercepción
|
-142,0812975
|
545,4130379
|
-0,260502202
|
0,80033868
|
|
|
PUBLICIDAD
|
1,367649015
|
0,892917686
|
1,531663037
|
0,15996695
|
|
|
PRECIO
|
46,47877955
|
31,36954818
|
1,481652821
|
0,17257378
|
|
|
|
|
a)
Determine al ecuación de regresión
b)
Interprete los coeficientes de regresión
c)
Cuántas ventas se espera con un precio de 40 y un
nivel de publicidad de 3000
|
|
|
|
|
|
|
|
|
Programa
| Objetivos | Distribución
del tiempo | Metodología | Laboratorio
| Evaluación | Cronograma
| Bibliografía | Enlaces
Inicio de la página
|