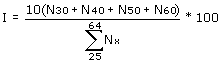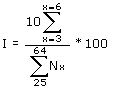Indice de Whipple: cuantificación de la exactitud en la declaración de la edad

Extraído de: Chackiel J y Macció G. (1978). Evaluación y corrección de datos demográficos. Centro Latinoamericano de Demografía (CELADE). Serie B, No 39. Agosto 1978. Santiago de Chile, Chile

Existen varios métodos para cuantificar la calidad de la declaración de la edad. Así es posible realizar comparaciones entre las declaraciones en los censos tanto a través del tiempo como del espacio. Para un país determinado podrá investigarse si de un censo al siguiente hay una mejora en la declaración, si ésta es mejor en zona urbana que en la rural, o para hombres que para mujeres, etc.

Existen los índices de Whipple, Myers, el de la Secretaría de las Naciones Unidas y el de usos de poblaciones estándar. Otros autores han elaborado índices un poco más complicados pero de menor uso, como es el caso de Bacchi, Michalup, Das Gupta, Carrier, Ramachandran, etc.

A continuación se describe el índice de Whiple o de concentración.

En su versión original está destinado a medir la preferencia por los dígitos 0 y 5 en conjunto, pero puede ser adaptado para establecer el nivel de atracción por cualquier dígito.

Así, si se deseara medir la preferencia por las edades terminadas en 0, el índice sería:

donde es la población en edad .

Bajo el supuesto que solo podría haber preferencias por el dígito 0, los resultados oscilarán entre un mínimo de 100 y un máximo de 1 000 en el caso que todos hayan declarado edades terminadas en 0, es decir cuando la concentración es máxima. Si el índice resultara menor que 100, estaría indicando un rechazo por el 0.

Este mismo índice, tal como se dijo, puede aplicarse para medir la atracción de cualquier dígito o de dos a la vez. Para las edades terminadas en 0 y 5 sería:

En general la versión más usada es ésta, que corresponde a la propuesta por Whipple.

El supuesto básico del índice es que la población correcta varía en forma lineal dentro de los grupos de edades 23-27, 28-32, 33-37....58-62:

El índice sería:

es decir, que cuando la información es exacta, de acuerdo a la hipótesis el índice vale 100 como se indicó anteriormente.

En el cuadro se muestran los índices de Whipple para los países de América Latina, Estados Unidos y Suecia en los censos de alrededor de 1950, 1960 y 1970. De acuerdo con una escala propuesta por las Naciones Unidas que plantea una asociación entre la preferencia de dígitos y la calidad de los datos censales, los países de la región, en su gran mayoría, tendrían información que fluctuaría entre mala y muy mala, aunque mejorando en el transcurso del tiempo, con tendencia a datos aproximados. Para 1970 se tendría, sin incluir Estados Unidos y Suecia, la siguiente distribución:

Por supuesto los índices de los dos países desarrollados, incluidos a título de comparación, corresponden al grupo de los “muy precisos”, no alcanzando en el último censo ni siquiera el valor 102.

En el cuadro se incluyen los índices correspondientes a la población de ambos sexos, pero también es posible realizar los cálculos para hombres y mujeres por separado.

PAÍSES DE AMÉRICA LATINA Y ESTADOS UNIDOS Y SUECIA:

INDICE DE WHIPPLE PARA LA POBLACIÓN TOTAL

a/ No se disponía de la información por grupos individuales de edades

b/ No existió censo

Regresar a Tarea sesión 2

Volver a la Sesión 2
Sesión siguiente

Inicio de la página