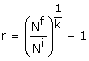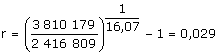|
Objetivos|
Cambios de estado|
Modelos matemáticos |Interpolación
y estrapolación|
Una vez finalizado el estudio de la presente sesión, el estudiante será capaz de:
¿Cuáles son los elementos que intervienen para que una población cambie de tamaño constantemente? En el primer capítulo se discutió sobre los principales determinantes del cambio demográfico y su efecto en el tamaño de una población. Se mencionó cómo, en cierto período de tiempo, el tamaño de una población puede crecer, mantenerse constante o disminuir, dependiendo del efecto que ejerzan estos determinantes o componentes de cambio. Estos agentes crean dos procesos dentro de la dinámica de una población. El primer proceso introduce nuevos elementos a la población y se conoce como proceso de entrada. En él intervienen la fecundidad o natalidad y la inmigración. El segundo proceso excluye individuos de la población, se conoce como proceso de salida, y en él intervienen la mortalidad y la emigración. Las relaciones entre estos dos procesos es la que provoca que el tamaño de la población esté expuesto a cambiar continuamente. De estas relaciones los demógrafos han establecido tres procesos de crecimiento:
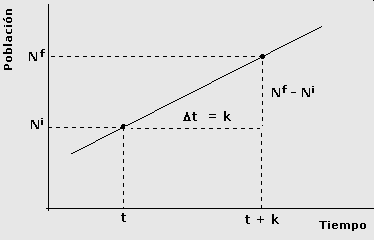
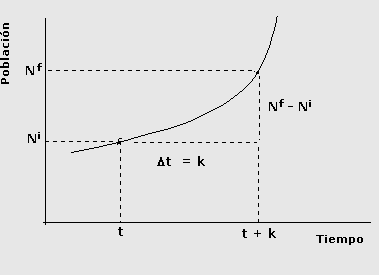
C(t,t+k) = CN(t,t+k) + SM(t,t+k) C(t,t+k) = B(t,t+k) - D(t,t+k)+ I(t,t+k) - E(t,t+k) Estas relaciones constituyen el principio básico de los análisis demográficos. En consecuencia el crecimiento de una población entre los momentos t y t+k viene dada por: Nt+k - Nt= C(t,t+k) con lo que: Nt+k = Nt+ C(t,t+k) Nt+k = Nt + B(t,t+k) - D(t,t+k)+ I(t,t+k) - E(t,t+k) Esta última ecuación recibe el nombre de ecuación compensadora del cambio demográfico, y como se verá a lo largo del curso, tiene gran cantidad de aplicaciones dentro del campo demográfico. ¿Cómo medir el ritmo de cambio del tamaño poblacional entre dos o más momentos? Porcentaje de crecimiento poblacional: Hasta el momento únicamente se ha analizado el incremento absoluto; pero este valor, por si solo, no permite valorar la verdadera magnitud del crecimiento alcanzado. Existen diferentes estrategias que permiten medir el ritmo de crecimiento de una población. Para ello se debe recurrir a una media relativa donde se eliminen los efectos de los tamaños poblacionales y del intervalo de tiempo correspondiente. La medida más simple consiste en el cociente: donde Ni: Representa la población del inicio del intervalo Nf: Representa la población al final del intervalo Este cociente permite medir el peso porcentual de la población final con respecto a la población inicial. Esta cifra presentan tres posibilidades:
Tasa de crecimiento poblacional:
Como se mencionó en la Tercera sesión, es posible
aproximar el tiempo vivido entre los momentos t y t+k por medio del
producto entre la población media " De esta manera, la tasa de crecimiento poblacional entre t y t+k se puede aproximar por cociente del crecimiento absoluto C(t,t+k) y la aproximación del tiempo vivido. Esta tasa se acostumbra representar con "r" y viene dada por: Con lo cual r = b - d + i - e o más simplemente r = b - d + sm donde b: Representa la tasa bruta de natalidad d: Representa la tasa bruta de mortalidad i: Representa la tasa bruta de inmigración e: Representa la tasa bruta de emigración sm: Representa la tasa de migración neta (sm = i - e) Del mismo modo, la tasa de crecimiento natural "r n" viene dada por: r n = b - d El siguiente cuadro presenta la información de los censos de Costa Rica desde 1950 hasta el año 2000. También se incluye el porcentaje de crecimiento poblacional entre los censos consecutivos y el tiempo transcurrido entre ellos. Costa Rica: Porcentaje de crecimiento y tasa de crecimiento en los períodos inter-censales. 1950-2000
Fuente: INEC. Censos nacionales del año 2000. San José, Costa Rica. www.inec.go.cr/INEC2/censo2000.pdf. 1
Para la determinación de estas tasas se utilizó la fórmula
como población media el promedio simple de los valores poblacionales.
r = (Nf - Ni)/(k· Se ha estimado que para el período 1984-2000 la tasa bruta anual de mortalidad y natalidad para Costa Rica fueron respectivamente de b = 0,026 y d = 0,004. Con estas cifras y el valor de r = 0,028 de la tabla anterior se tiene que: r n = 0,026 - 0,004 = 0,022 sm = 0,028 - 0,022 = 0,004 El crecimiento vegetativo anual de Costa Rica durante el período 1984-2000 fue de 22 personas por cada mil habitantes. Mientras que el saldo migratorio neto en este mismo período fue de 4 personas por cada mil habitantes. Se debe aclarar que estos datos suponen que no existen errores en el registro de estadísticas vitales ni de cobertura en los datos censales. Una de las aplicaciones de mayor interés que tienen estos conceptos, lo constituye la evaluación de la información censal. Desafortunadamente, para ello se requiere contar con información sobre migración. A manera de ejemplo, considere la siguiente información para Costa Rica.
1 Obtenido por una proyección del Censo de población 1984 2 Información obtenida por medio de CELADE. La población de Costa Rica estimada al 1 de enero de 1984 es: N01/01/84 = 1 902 093 + 663 910 - 96 018 + 50 000 = 2 519 985 Si lo que se pretende es evaluar el censo de población de 1984, esta información indica que se presentó una diferencia de aproximadamente 130 000 habitantes entre el valor del censo y el valor estimado por esta técnica. Suponiendo los datos como válidos, se observa una sub-enumeración en el censo de 1984 en aproximadamente 5,2%. Una tasa de crecimiento poblacional puede ser estimada suponiendo que este crecimiento sigue cierto patrón preestablecido. Los análisis más utilizados en demografía parten del supuesto de que la población sigue cierto modelo matemático, y el procedimiento consiste en estimar la relación funcional que lo explica. Generalmente se consideran tres modelos básicos: Modelo aritmético: Es el más simple de todos. Supone que la población tiene un comportamiento lineal y por ende, la razón de cambio también se supone constante, es decir se incrementa en la misma cantidad cada unidad de tiempo considerada.
Puesto que la razón de cambio se supone constante y si "r" es la tasa de crecimiento por unidad de tiempo, entonces el crecimiento de la población entre un momento t y un momento t + k viene dada por: DN= Ni · r · k Entonces la población en el momento t + k sería: Nf = Ni + DN es decir, Nf= Ni + Ni · r · k Nf= Ni (1+ r · k) Si se despeja el valor de "r" en la ecuación anterior, se obtiene la fórmula para la tasa de crecimiento bajo el supuesto aritmético: Si se considera nuevamente la información de los censos de Costa Rica, particularmente los dos últimos, se tiene que bajo el supuesto aritmético su tasa de crecimiento sería:
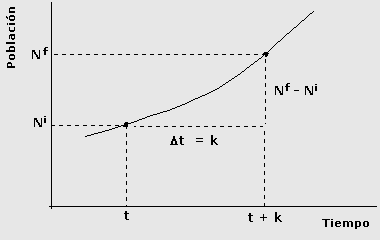
Modelo geométrico: En el modelo aritmético el supuesto básico consiste en que la población crece en un mismo monto cada unidad de tiempo. En el modelo exponencial se mantiene constante el porcentaje de crecimiento por unidad de tiempo y no el monto.
Supongamos que "r" es la tasa de crecimiento por unidad de tiempo, el tamaño de la población en la primera unidad de tiempo está dado por: N1= Ni + Ni · r = Ni ·(1 + r) Para la segunda unidad de tiempo: N2= N1 + N1 · r = N1 ·(1 + r) = [Ni ·(1 + r)]·(1 + r) =Ni ·(1 + r)2 Para la tercera unidad de tiempo: N3= N2 + N2 · r = N2 ·(1 + r) = [Ni ·(1 + r)2]·(1 + r) =Ni ·(1 + r)3 Generalizando este resultado para el momento t + k, la población sería; Nf= Ni ·(1 + r)k Nuevamente si de despeja el valor de "r" en esta ecuación, se obtiene la fórmula para la tasa de crecimiento poblacional bajo el supuesto geométrico:
Al repetir el ejemplo hecho para el caso aritmético, bajo el supuesto geométrico, la tasa de crecimiento poblacional para el período 1984-2000 es:
Modelo exponencial: A diferencia del modelo geométrico, el modelo exponencial supone que el crecimiento se produce en forma continua y no cada unidad de tiempo. Este supuesto obliga a sustituir la expresión "(1 + r)k" por "er·t" o "Exp(r·t)". La justificación de esta sustitución se fundamenta en principios del Cálculo matemático, y su demostración sobrepasa los objetivos de este curso.
El tamaño de la población en el momento t + k viene dado por: Nf= Ni ·er·k = Ni · Exp(r·k) entonces, la tasa de crecimiento poblacional bajo este supuesto viene dada por:
Bajo este modelo, la tasa de crecimiento poblacional para el período 1984-2000 es: Como puede notarse, esta tasa es similar al obtenido por la fórmula general:
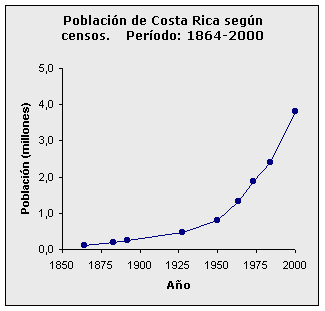
cuyo valor aparece en la tabla dada arriba. Si se analiza gráficamente el crecimiento experimentado por la población de Costa Rica desde el año 1864:
Fuente: INEC. Censos nacionales del año 2000. San José, Costa Rica. www.inec.go.cr/INEC2/censo2000.pdf. Claramente puede observarse que efectivamente, el crecimiento experimentado por esta población sigue un patrón que se asemeja a una función exponencial, por lo que se podría concluir que, al menos entre 1960 y el año 2000, el modelo que mejor explica el comportamiento de la población de Costa Rica es el exponecial. ¿Cuánto tiempo requiere una población para duplicar su tamaño? La respuesta a esta pregunta requiere de una serie de hipótesis sobre el comportamiento futuro de la población. Los métodos más simples consisten en suponer, que el crecimiento de la población sigue un modelo matemático similar a los estudiados anteriormente. Para aplicar cualquiera de estos métodos se requiere conocer la tasa de crecimiento de la población y suponer que permanece constante en el futuro. Bajo estos supuestos la determinación del tiempo de duplicación se obtiene de un simple despeje matemático sustituyendo Nf con 2Ni. En la siguiente tabla se presentan las ecuaciones que permiten estimar el tiempo de duplicación de la población bajo los tres supuestos matemáticos.
Por razones prácticas el modelo que es utilizado en mayor medida por los demógrafos es el exponencial. A continuación se detalla el tiempo de duplicación del tamaño de la población de Costa Rica, a partir del año 2000 y bajo las hipótesis de un crecimiento similar al que se presentó en el período 1984-2000.
Estos tres modelos señalan que si la población de Costa Rica continúa creciendo al ritmo que lo hizo en el período 1984-2000, duplicaría su tamaño antes del año 2030. ¿Cómo poder estimar el tamaño de una población en períodos inter-censales y post-censales? Interpolación y extrapolación: Los modelos matemáticos que se han utilizado anteriormente pueden ser utilizados para estimar el tamaño de una población en un momento concreto, ya sea en un memento entre dos censos o predecir el tamaño que esta población podría tener o haber tenido, en un momento futuro o pasado respectivamente. Para ello se deben considerar las mismas hipótesis analizadas antes. Cuando la estimación se realiza para un momento entre dos puntos conocidos (dos censos) se llama interpolación; pero cuando se realiza hacia el futuro o hacia el pasado de un período conocido, se le llama extrapolación. Por ejemplo, supóngase que se desea estimar la población de Costa Rica, bajo los tres modelos básicos, para el 30 de junio de 1990 y para el 30 de junio del año 2010. El siguiente cuadro presenta un resumen de los elementos más importantes que deben considerarse para efectuar estas estimaciones.
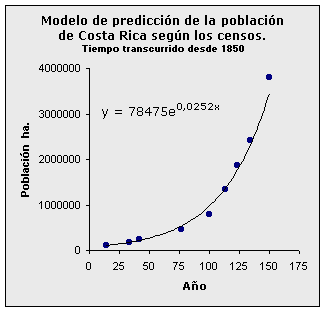
Sin embargo, existen muchas otras técnicas matemáticas que permiten efectuar interpolaciones y extrapolaciones. Las que se han desarrollado hasta el momento parten del conocimiento de dos puntos; sin embargo, muchas otras técnicas requieren de más de un punto para estimar el modelo funcional, que puede ser utilizado en las predicciones. Basados en principios matemáticos y estadísticos, es posible aproximar funciones que realicen predicciones fundamentadas en una serie de puntos u observaciones. Con las actuales herramientas tecnológicas no es necesario saber mucha matemática para poder poner en práctica estos principios. Con una simple "hoja de cálculo" (Microsoft Excel) es posible determinar un modelo matemático que ajuste una serie de puntos de una manera muy acertada. A modo de ejemplo, si se considera la población Costa Rica de acuerdo con los nueve censos de población efectuados, es posible por medio de Microsoft Excel generar un modelo matemático, que permita estimar la población a partir de 1850.
De este modo el modelo matemático generado por el programa es: Nt = 78475·e0,0252·t (t es número de años trascurridos desde 1850) Con este modelo para el año 1990 (t = 140) la población de Costa Rica era de: N1990 = 78475·e0,0252·140= 2 672 528 Mientras que para el año 2010 (t = 160) la población de Costa Rica sería de: N2010 = 78475·e0,0252·160= 4 423 914 De acuerdo con los resultados del último censo, pareciera que este modelo subestima el valor poblacional, sobre todo en los años en que se efectuaron las estimaciones; no obstante, es una muy buena aproximación matemática sobre el comportamiento de la población de Costa Rica en los últimos 150 años.
Objetivos|
Cambios de estado|
Modelos matemáticos |Interpolación
y estrapolación|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||