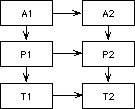
Programación por camino crítico.
Un proyecto es un conjunto de tareas relacionadas entre sí. Cada tarea tiene algún tipo de prioridad respecto de otra. Es decir existe antecedencia y consecuencia entre las tareas.
Supongamos el siguiente proyecto:
Se debe tender una línea telefónica a lo largo de una ruta. Para esto se debe: a) hacer agujeros, b) erguir postes y finalmente c) tender la línea. Con fines operativos dividimos a la ruta en dos sectores (1 y 2). Tenemos un equipo capaz de cavar, otro de postear y otro de tender la línea.
El esquema de prioridades es el que sigue:

Donde:
A1 : Agujereado del sector 1A2 : Agujereado del sector 2
P1 : Posteado del sector 1
P2 : Posteado del sector 2
T1 : Tendido del sector 1
T2 : Tendido del sector 2
Asegúrese de haber comprendido el esquema.
Realizaremos una red, con los conocimientos que tenemos sobre grafos, con la siguiente convención: Las tareas serán simbolizadas por medio de arcos y los sucesos por medio de nodos. Los sucesos denotan el comienzo y la finalización de cada tarea.
Note que cada nodo tiene un nombre n
![]()
Luego nombrar a la tarea AB es lo mismo que referirse a la tarea A1.
Una tarea como la CE recibe el nombre de Ficticia (dado que no es real) y se necesita para mostrar la lógica del proyecto. Halle el error en el diagrama que sigue:
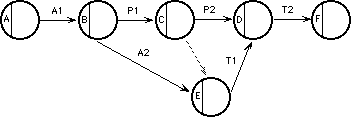
Exprese que indica cada uno de estos nodos.(ninguno indica menos de dos sucesos)
Trate de mostrar este mismo proyecto mediante otra gráficas. En todos los casos verifique que se cumpla la lógica del mismo.
Fecha temprana
![]()
Colocamos las duraciones de cada tarea sobre los arcos correspondientes. Comenzamos el proyecto en el día 0. Comenzamos la tarea AB el día 0. En los ejemplos dados aquí supondremos siempre que la duración está expresada en días.
¿Cuál es la fecha más temprana que puedo estar en el suceso B, para comenzar con BC y BE?
(El suceso B indica la finalización de AB, el comienzo de BC y el comienzo de BE)
Obviamente el día 2, que es el tiempo que tardamos en hacer AB.
La situación queda representada así:
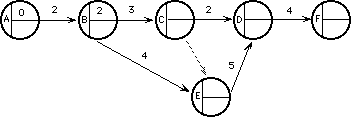
¿Cuál es la fecha más temprana que puedo estar en el suceso C, para comenzar CD?
(El suceso C indica la finalización de BC, el comienzo de CD y el comienzo de ED).
Obviamente el día 5, que es el tiempo que tardamos en hacer BC, más lo que tardamos estar en B ( 3 + 2 = 5 ).
La situación queda representada así:
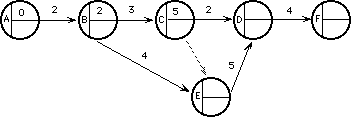
¿Cuál es la fecha más temprana que puedo estar en el suceso E, para comenzar ED?
(El suceso E indica la finalización de .........., y de........el comienzo de .........).
Debemos decidir entre 5 y 6 .Determinamos que la fecha más temprana para comenzar ED es 6.
Explique porqué.
La situación queda representada así:
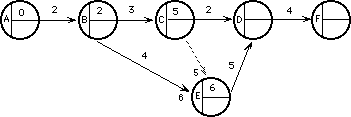
¿Cuál es la fecha más temprana que puedo estar en el suceso D, para comenzar con DF?
Dedúzcalo convenientemente.
La situación queda representada así:
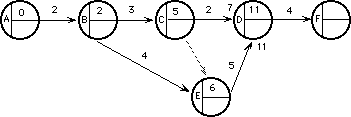
¿En que fecha llegamos al suceso F, terminando el proyecto y la tarea DF ?
Dedúzcalo convenientemente.
La situación queda representada así:
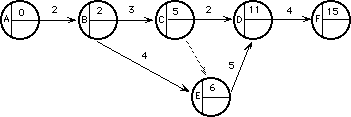
Nuestro proyecto se puede realizar en 15 días. El menor tiempo que necesitamos para realizar el proyecto es de 15 días.
Fecha tardía
![]()
La última fecha que tenemos para finalizar la tarea DF ( y el proyecto ) es el día 15.
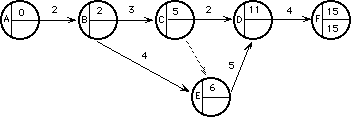
¿ Cuál es la fecha tardía para comenzar con la tarea DF ? 9. ( 15 - 4 = 9).
Supongamos que la comienzo el día 12. Entonces : 12 (suceso D) más 4 (duración DF) hace que e proyecto termine el día 16, es decir un día más tarde.
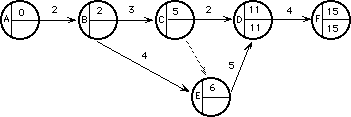
Aplique el mismo criterio para comenzar con la tarea ED.
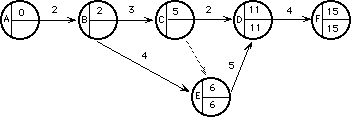
¿Cuál es la fecha tardía para el suceso C ? Debemos elegir entre ( 11 - 2 = 9) y
( 6 - 0 = 6).Recuerde que la duración de una tarea ficticia es 0 (no existe como tarea real).
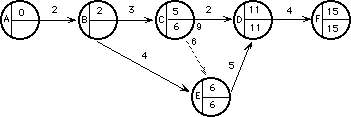
Aplique el mismo criterio para hallar la FT de las tareas BC y BE.
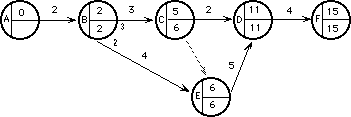
Determine la fecha tardía del suceso A.
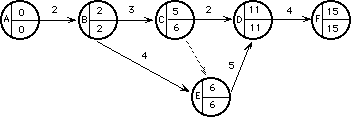
Analicemos las fechas de la tarea CD
ftc : 5FTC : 6
ftf : 11
FTF : 11
Analice las tareas restantes con este mismo criterio
Sucesos críticos
Un suceso crítico es aquel cuyas ft y Ft son iguales.
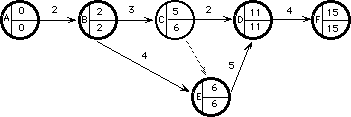
Tareas críticas
Son aquellas cuya duración es igual a la diferencia entre los sucesos críticos que la determinan.
Se encuentra entonces el camino crítico. (Subgrafo crítico)
Estas son las tareas que hacen que el proyecto dure 15 días.
Luego si se incrementa la duración de alguna de estas tareas, se incrementará la duración del proyecto.
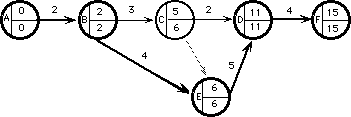
Hasta ahora calculamos tiempos del proyecto. Note que la longitud de los arcos no es proporcional a la duración de a tarea.
Esta proporción se puede mostrar en el diagrama calendario.
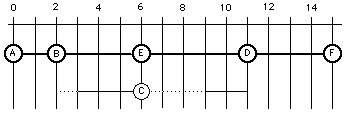
Se construye de la siguiente manera: primero se colocan los sucesos críticos en su fecha correspondiente e inmediatamente se grafican las tareas críticas.
Luego se colocan los otros nodos. En este caso colocamos el nodo C en su ft. El que sigue se denomina Diagrama calendario de ft.
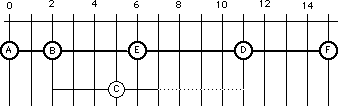
Note el margen de la tarea CD (línea punteada). Indica la cantidad de días que podemos atrasarnos en esa tarea sin atrasar el proyecto.
El que sigue es el Diagrama calendario de FT.
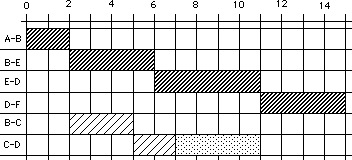
El esquema que sigue se denomina Diagrama de Gantt de ft, con prioridad de Camino Crítico.
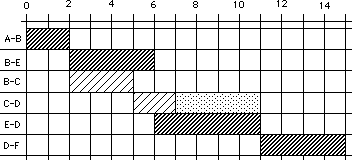
El esquema que sigue se denomina Diagrama de Gantt de ft, con prioridad de fechas
El esquema que sigue se denomina Diagrama de Gantt de FT, con prioridad de fechas.
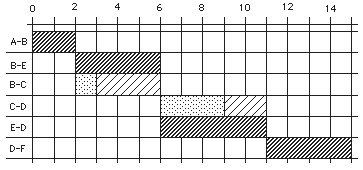
Note que en estos esquemas no aparece la tarea ficticia. Determine el motivo.
Hasta aquí se ha visto el algoritmo que permite calcular las fechas para cada tarea y al asignar estas duraciones se habló de "tiempo" en forma general.
Sucede, que en particular existen tres tipos de tiempos, que se obtienen en base a la experiencia anterior sobre cada tipo de tarea. Son:
![]() : Tiempo óptimo
: Tiempo óptimo
Es la menor duración histórica de esa tarea.
![]() : Tiempo modal
: Tiempo modal
Es la duración de mayor frecuencia histórica de esa tarea.
![]() : Tiempo pésimo
: Tiempo pésimo
Es la mayor duración histórica de esa tarea.
Ejercitación P.E.R.T
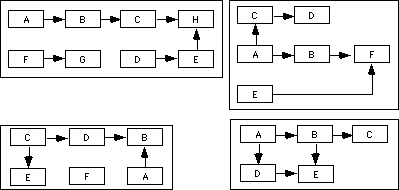
Realice la red correspondiente a cada uno de los cuatro proyectos que siguen. Recuerde las distintas formas de verificación y ejercítelas.
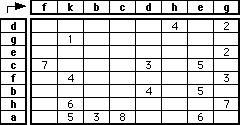
Dada la siguiente matriz:
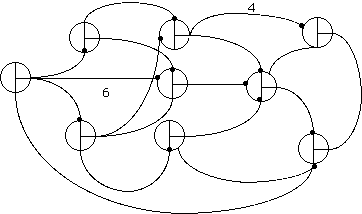
Critique el diseño de la red, pero úsela para determinar el camino crítico.(Antes corrija los errores más gruesos)
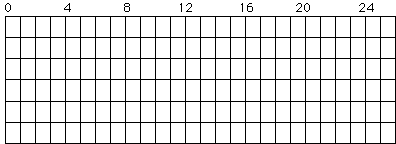
Determine el diagrama de Gantt para fechas tempranas.
Determine el diagrama de Gantt para fechas tardías.

La red que sigue ha sido diseñada con la norma opuesta a la utilizada a nivel local, es decir distinta a la aprendida hasta ahora en el curso.
Por las dudas: los nodos representan tareas y los arcos la vinculación entre ellas.
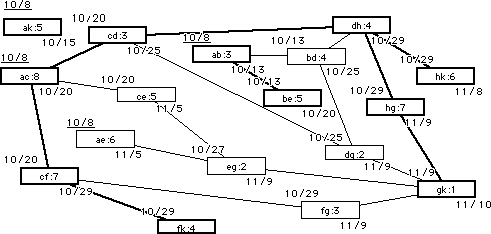
Determine por qué pese a ser el mismo proyecto que el antes resuelto, este al comenzar el ocho de octubre de 1993 finaliza el diez de noviembre del mismo año. Discuta sobre los inconvenientes, si existen, de este tipo de diseño.
A continuación se muestran los tiempos modales, óptimos y pésimos, realmente no se en que orden, de las tareas que componen un pequeño proyecto.
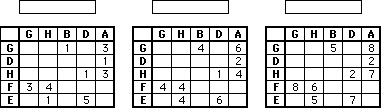
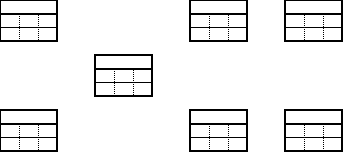
Critique el esquema de nodos propuesto.
Determine las redes correspondientes las distintas duraciones.