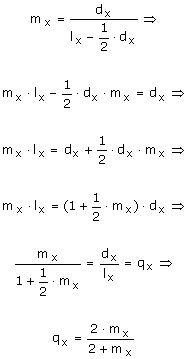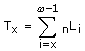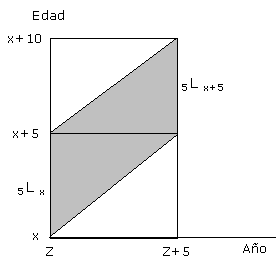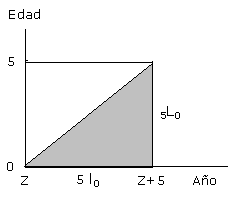Sesión 8

8. Tablas de vida

Bajar para imprimir

Objetivos

Una vez finalizado el estudio de la presente sesión el estudiante será capaz de:

• Definir el concepto de tabla de vida y sus principales características.

• Valorar la importancia de las tablas de vida para de los análisis demográficos y de otras áreas.

• Definir e interpretar las principales funciones de una tabla de vida: l_x, d_x, q_x, p_x, k_x, L_x, T_x y e_x.

• Representar gráficamente las distintas funciones de una tabla de vida e interpretar sus patrones básicos.

• Establecer las relaciones entre las distintas funciones de la tabla de vida.

• Establecer la relación entre las tasas centrales de mortalidad y las probabilidades de muerte.

• Construir una tabla de vida a partir de las tasas centrales de mortalidad.

• Calcular e interpretar las relaciones de sobrevivencia generadas de una tabla de vida.

• Reconocer la importancia de las tablas modelo para la construcción de tablas de vida en países con datos poco confiables.

• Reconocer las principales aplicaciones prácticas de una tabla de vida.

¿Qué es una tabla de vida?

Una tabla de vida o tabla de mortalidad, es un modelo teórico que describe la extinción de una cohorte hipotética o ficticia. Permite determinar las probabilidades de sobrevivir o de morir a una edad exacta "x" o entre edades "x" y "x+n". Se considera como la herramienta más completa para el análisis de la mortalidad de una población en un momento dado. Los supuestos fundamentales para la creación de una tabla de vida son:

• Es un modelo teórico que describe, numéricamente, el proceso de extinción por muerte de un grupo inicial, generalmente una cohorte de de recién nacidos (base de la tabla).

• La ley de extinción corresponde a la mortalidad experimentada por una población durante una período de tiempo específico relativamente corto (generalmente un año).

• La mortalidad se plantea en función de la edad y sus patrones (m_x) se consideran constantes en el tiempo.

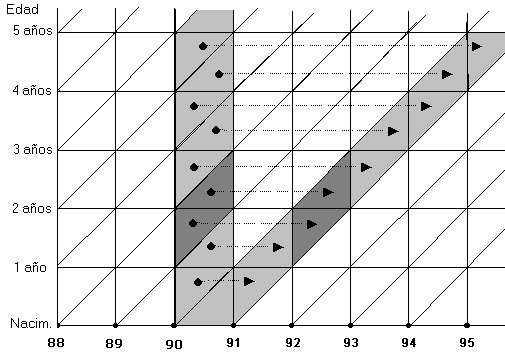
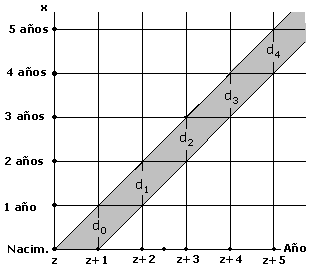
En realidad la una tabla de vida es una análisis transversal, dado que se basa en el patrón de mortalidad actual observada sobre los miembros de una población real, por lo que se refiere a un análisis transversal. Por esta razón se le llama "tabla de contemporáneos", a diferencia de una "tabla de generaciones", la cual se basa en un análisis longitudinal de la mortalidad de una generación específica, desde su nacimiento hasta su extinción completa. En este último caso, se requiere de un período de al menos 100 años para concluir el estudio, lo cual lo hace improbable e ineficiente. En la tabla de contemporáneos los patrones de mortalidad para la cohorte en estudio, corresponden en realidad a las distintas generaciones en el mismo momento, tal como lo muestra el siguiente diagrama de Lexis para el año 1990.

El diagrama por medio del análisis transversal se puede simular el comportamiento longitudinal de la generación de l990. Por ejemplo, las defunciones de la generación de 1988 ocurridas en el año 1990, van a representar las defunciones de la cohorte de 1990 y que ocurren en el año 1992. Del mismo modo se efectúa una simulación de las defunciones en las restantes cohortes.

¿Cuáles son las principales características de una tabla de vida?

Las tablas de vida se caracterizan por:

• Permiten describir el comportamiento de la mortalidad por edades y hacer comparaciones por sexo.

• Permiten obtener probabilidades de mortalidad, las cuáles son más apropiadas que las tasas de mortalidad (m_x) para realizar diferentes análisis demográficos.

• Permite calcular la esperanza de vida para las diferentes edades o grupos de edad. Como se mencionó en la sesión anterior ésta es una de las principales medidas resumen de mortalidad, pues no esta afectada por la estructura por edades de la población.

• Puede ser llevada a un modelo teórico de población, llamado población estacionaria, la cual se logra manteniendo constantes en el tiempo la mortalidad y la natalidad. En ella la tasa de natalidad es igual a la tasa de mortalidad y la tasa de crecimiento es 0.

• Permite efectuar diversas aplicaciones en gran variedad de problemas tales como: estimación del nivel y tendencia de la mortalidad, evaluación de programas de salud, estudios de fecundidad y migración, estudios socioeconómicos como fuerza de trabajo, población escolar, regulación en sistemas de jubilaciones, etc.

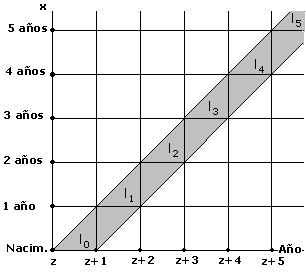
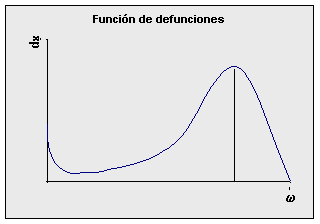
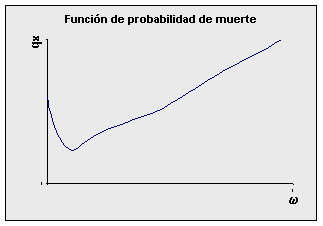
Como se ha venido mencionando se pueden crear tablas de vida para edades simples o para grupos de edad. Cuando se trabaja por grupos de edades, el grupo más común es el quinquenal; sin embargo, debido a las fuertes diferencias en mortalidad que se presentan en los primeros años de vida, se recomienda que el primer grupo se presente en forma individual, especialmente a la edad 0.

¿Cuáles son los elementos que se incluyen en una tabla de mortalidad?

Para construir una tabla de mortalidad se debe considerar una serie de funciones con respecto a la edad. Cada una de estas funciones tiene muchas aplicaciones dentro del campo demográfico, por lo que conviene tener una clara compresión de ellas, así como su fórmula de cálculo y su interpretación. A continuación se detalla el comportamiento de cada una.

Función de sobrevivientes: l_x

Esta función representa el número de personas de la generación inicial que llegaron con vida a la edad exacta "x". El valor l₀ representa el tamaño de la cohorte inicial (nacimientos) y se conoce como "raíz de la tabla". Como se esta trabajando con un modelo teórico, se acostumbra trabajar con una raíz de 100 000. Por otro lado, se acostumbra representar con w (omega)la edad a la que muere el último miembro de la generación, por lo que l_w= 0. En un diagrama de Lexis se puede apreciar como los valores l_x corresponden a la base de cada paralelogramo.

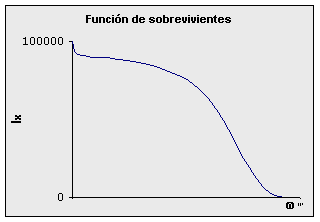
La función l_x es decreciente y presenta una curvatura hacia arriba en los primeros años debida a la fuerte mortalidad. A continuación se presenta el comportamiento gráfico básico de esta función:

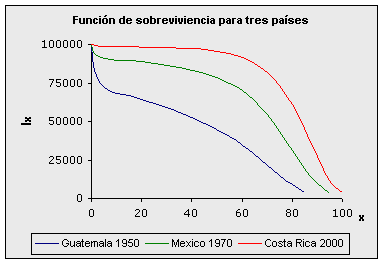
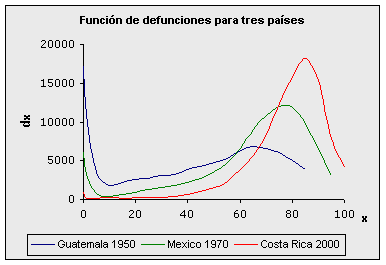
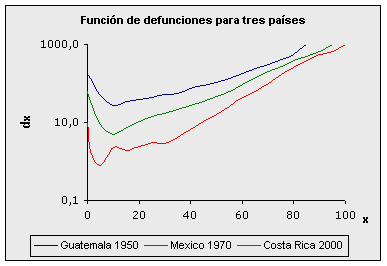
El valor de w puede ser muy grande, incluso superior a los 100 años, pero generalmente se trabaja con la población de las últimas edades en forma agrupada. Por lo general las tablas se construyen hasta una edad suficientemente alta, 85, 90 o 95 años, dejándose luego el grupo abierto.

La forma de la curva va a depender del patrón de mortalidad que se presenta en la población. A continuación se presenta la función de sobreviviencia de acuerdo con el patrón de mortalidad masculina de Guatemala en 1950, femenina de México en 1970 y femenina de Costa Rica en el año 2000.

Fuentes: Camisa, Zulma. Las estadísticas demográficas y la mortalidad en Guatemala hacia 1950 y 1964. CELADE, serie AS No 2, San José, Costa Rica, 1969. Cabrera, Gustavo y otros. Tabla abreviada de mortalidad de México, 1969-1971. El Colegio de México, C:E.E.D., 1973. Ambos presentados en Ortega, Antonio. Tablas de Mortalidad. CELADE. San José, Costa Rica, 1987. ccp.ac.cr

Observe que a medida que el patrón de mortalidad de la población disminuye, la curva tiende a asemejarse a un rectángulo.

La función l_x tal como se ha definido se puede interpretar también como la probabilidad de llegar con vida a la edad "x" por 100 000. Por ejemplo si l₂₀ = 88 775 entonces se puede decir que la probabilidad de llegar con vida a los 20 años es de aproximadamente 0,89 u 89%.

Función de defunciones: d_x

Esta función representa el número de defunciones de la generación inicial ocurridas entre las edades "x" y "x+n". Debe observarse que estas defunciones corresponden a una cohorte hipotética, por lo que se les llama "defunciones de la tabla" a diferencia de las defunciones observadas en la población real. De lo anterior se deduce que

d_x = l_x - l_x+1

En un diagrama de Lexis se puede representa los valores d_xa lo largo de la franja correspondiente a la cohorte de interés. El área de cada paralelogramo de la figura representa las defunciones entre x y x+1 para la cohorte correspondiente al año Z.

Si se trabaja con grupos de edades en vez de edades simples entonces la función de defunciones se denota con _nd_x, donde "n" representa el el número de años del grupo (generalmente se utilizan grupos quinquenales). Se interpreta como el número de defunciones de la generación inicial ocurridas entre las edades "x" y "x+n" . En este caso la función de defunciones se puede calcular por:

_nd_x = l_x - l_x+n

La representación gráfica de esta función se muestra a continuación:

La edad donde la función d_x alcanza el valor máximo se conoce como edad modal de las defunciones. A esta edad es donde se produce la mayor cantidad de muertes, a medida que los patrones de mortalidad disminuyen, la edad modal de la mortalidad aumenta, generalmente varía entre los 65 y los 85 años. Este comportamiento se puede observar mejor en las gráficas correspondientes a los patrones de los tres países que se estudiaron antes.

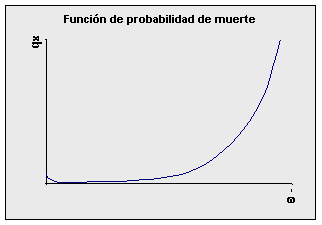
Mientras en Guatemala en 1950 la edad modal es alrededor de 60 años, en México en 1970 esta alrededor de los 76 años y en Costa Rica supera lo 80 años.

Función de probabilidad de muerte: q_x

Esta función va a representar la probabilidad asociada a que una persona perteneciente a la cohorte hipotética muera a la edad cumplida x (muera en el año comprendido entre edades "x" y "x+1"). De acuerdo con el concepto de probabilidad se tiene que, q_x es una relación entre d_x y l_x, es decir una relación entre los casos favorables (defunciones ocurridos a la edad cumplida "x")y el total de casos (sobrevivientes a la edad "x").

Su comportamiento gráfico se asemeja mucho al obtenido cuando con las tasas específicas de mortalidad por edad.

Escala normal
Escala logarítmica

A continuación se muestra el comportamiento de la función de probabilidad de muerte para los tres modelos que se han venido observando.

Las diferencias entre patrones de mortalidad de cada año y para cada país quedan claramente evidenciados en este gráfico.

Cuando se trabaja con grupos de edades, la probabilidad de muerte entre las edades "x" y "x+n" se representa con _nd_x y se calcula mediante la fórmula:

La función de mortalidad aplicada al primer año, q₀ representa la probabilidad de morir durante el primer año de vida, la cual como se analizó en la sexta sesión un estimado de la tasa de mortalidad infantil.

Aunque durante el desarrollo previo, pareciera que para calcular las probabilidades de morir se requiere conocer el comportamiento de d_x o en su defecto l_x; sin embargo, el proceso es contrario, se requiere conocer el valor de las probabilidades de morir en cada edad o grupo de edades para generar los valores de las funciones l_x y d_x. De este modo, a partir del valor l₀ y de los valores de q_x se obtiene los valores de las otras dos funciones, mediante el proceso siguiente:

Por esta razón, en el proceso de construcción de una tabla de vida se requiere conocer estas probabilidades de defunción. Sin embargo; éstas pueden ser generadas a partir de las tasas especificas de mortalidad por edad simple o grupo de edades. De acuerdo con las sesiones anteriores, si m_x es la tasa de mortalidad para la edad cumplida "x", entonces:

Donde representa la población media de edad cumplida "x" y es un aproximada del tiempo vivido por esta población durante un año. Bajo el supuesto que para edades de 5 o más años (x ³ 5), las defunciones se presentan aleatoriamente durante el año, la población media puede ser aproximada por:

Entonces:

Para las primeras edades (x = 0, 1, 2, 3, 4) la fórmula anterior no se puede aplicar pues, como se ha discutido ampliamente la mortalidad en las primeras edades se comporta en forma muy diferente al resto. Para x = 0, se asume que q₀ = TMI y para las restantes edades se debe buscar una una función f_x llamado factor de separación de las defunciones, el valor de f_x corresponde a la proporción de defunciones de edad cumplida "x" que se presentan en la segunda mitad del año. Por lo que el tiempo vivido por la generación entre las edades "x" y "x+1" viene dado por:

Utilizando esta fórmula se puede se puede obtener nuevamente la relación entre las tasas específicas de mortalidad por edad "m_x" y la probabilidad de muerte "q_x".

Esta fórmula puede ser aplicada para todas las edades, solo que en los casos en los que x ³ 5 se supone que f_x = 0,5. El factor de separación para las primeras las edades de 1 a 4 años, es también un valor cercano a 0,5; sin embargo, es difícil de calcular su valor. En algunas ocasiones se han utilizado los llamados factores de separación de Glover, obtenidos con base en estadísticas de Alemania a comienzos del siglo XX.

	Factores de separación de Glover
x	1	2	3	4
f_x	0,41	0,47	0,48	0,48

Fuente: Greville, Thomas. United States Life Tables and Actuarial Tables 1939-1941. United States, Departament of Commerce, Bureau of the Census, Washington, 1946. Presentados en Ortega, Antonio. Tablas de Mortalidad. CELADE. San José, Costa Rica, 1987. Presentados en

A manera de ejemplo, el siguiente cuadro muestra las probabilidades de defunción para las primeras 7 edades determinadas por la formula anterior, bajo el supuesto que se conoce la TMI y las tasas específicas de mortalidad para esas edades:

x	m_x	f_x	q_x
0	0,039837	-	0,037911 (TMI)
1	0,004251	0,41	0,004240
2	0,001977	0,47	0,001975
3	0,001127	0,48	0,001126
4	0,001084	0,48	0,001083
5	0,000796	0,50	0,000796
6	0,000642	0,50	0,000642

Si se trabaja con grupos de edades en vez de edades simples, entonces las fórmulas anteriores deben sufrir ciertas variantes. La aproximación del tiempo vivido sería:

donde la función _nf_x corresponde al factor de separación anual del grupo de edades "x" a "x+n". Sin embargo; aunque se trabaje con grupos de edades se recomienda trabajar con el primer grupo con la edad 0 y el siguiente de 1 a 4 años. Para estos casos se tiene que:

y realizando un despeje similar al efectuado para las edades simples se tendría:

Si se trabaja con grupos quinquenales, en el grupo de 1 a 4 años se puede utilizar un valor de ₄f_x cercano a 0,35, mientras que para los restantes grupos se supone que ₅f_x = 0,5.

Edad	_nm_x	_nf_x	_nq_x
0	0,039837	-	0,037911 (TMI)
1-4	0,002125	0,35	0,008453
5-9	0,000644	0,50	0,003215
10-14	0,000490	0,50	0,002447
15-19	0,000861	0,50	0,004296

95 y más	0,361516	-	1,000000¹

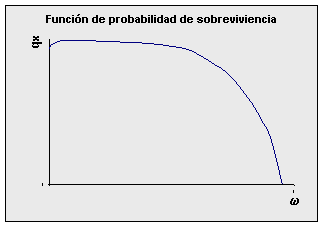
¹ Observe que la probabilidad de morir en el último grupo es uno, lo cual es evidente.

Función de probabilidad de sobrevivencia: p_x

A partir de las probabilidades de muerte q_x o _nq_xse pueden definir las probabilidades de sobrevivencia p_x o con _np_x, la cual representa la probabilidad de sobrevivir entre las edades "x" y "x+1" o entre "x" y "x+n" respectivamente. La función de sobrevivencia se define por:

para el caso de edades simples o por:

para el caso de grupos de edades de tamaño "n". La representación grafica de la función se muestra a continuación:

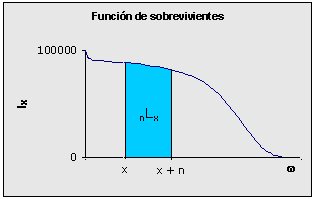
Para mayor facilidad se puede determinar la probabilidad de sobrevivencia por medio de las fórmulas: p_x = 1 - q_x o _np_x = 1 - _nq_x.

Función de tiempo vivido: L_x

Esta función corresponde al tiempo que vive toda la generación entre las edades "x" y "x+1" o entre las edades "x" y "x+n". El principal problema está en determinar el valor de esta medida radica en evaluar el aporte en tiempo vivido de las personas que mueren entre estas edades. Como bien se discutió en el punto anterior, la función tiempo vivido puede ser estimada, respectivamente para edades simples o grupos de edades, por medio de las fórmulas:

El valor de esta función representa el área comprendida bajo la representación gráfica de l_x entre las edades "x" y "x+1" o entre "x" y "x+n" según se trabaje con edades simples o grupos respectivamente.

De acuerdo con lo discutido anteriormente, en algunos casos se puede suponer que las muertes se producen aleatoriamente a lo largo de un año o de un período de n años y, por ello, se puede asumir que cada persona que murió en este período aporta la mitad del tiempo que dura el período, por lo que f_x sería igual a 0,5. Pero también se discutió que esto no es cierto para las primeras edades o para el primer grupo de edades y tampoco para el grupo abierto del final. Se utilizar la fórmula:

para despejar el valor f₀, por lo que se obtiene que:

Sin embargo; para poder utilizar esta fórmula se requiere que q₀ y m₀ sean valores muy confiables, lo cual no siempre es cierto.

En general, si se tiene confianza con respecto a las tasas específicas de mortalidad por edad, se puede utilizar la relación:

para despejar el valor correspondiente al tiempo vivido, con lo cual se tendría que:

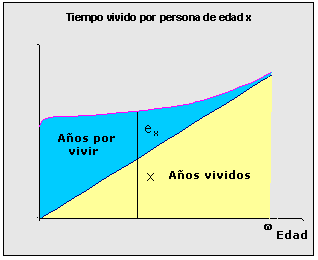
Función de tiempo vivido entre x y w: T_x

A diferencia de la función anterior esta función corresponde al tiempo que le falta por vivir a la generación hasta su extinción. Una manera práctica de definir T_x es:

Gráficamente el valor de T_xcorresponde al área bajo la curva de l_x desde x hasta w.

Función esperanza de vida a la edad x: e_x

Como ya se ha definido antes, la esperanza de vida para una persona de edad "x", corresponde al número promedio de años que le restaría por vivir. Su valor se obtiene de la razón entre el número de años que le resta vivir a la generación completa a partir de la edad "x" entre el número de sobrevivientes a esta edad.

Un valor muy particular de esta función corresponde a la esperanza de vida al nacer, la cual es una medida resumen de la mortalidad de un país o de una región. Como ya se ha dicho es un excelente indicador de la mortalidad pues no está afectado por la estructura por edad de la población y es especial para comparar los niveles de la mortalidad entre países o regiones. Su comportamiento gráfico se muestra a continuación:

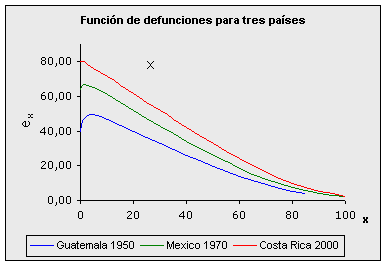
Generalmente la esperanza de vida al nacer es inferior a la obtenida en los primeros años, esto es más evidente cuando el patrón de mortalidad es muy alto. Para ejemplificar esta situación el siguiente gráfico el comportamiento de la esperanza de vida en las tres poblaciones que se han venido analizando.

El gráfico muestra el comportamiento de la esperanza de vida conforme disminuye la mortalidad. Mientras que los varones en Guatemala en 1950, aparte de una baja esperanza de vida, su valor máximo se alcanza cerca de los 5 años, las mujeres de Costa Rica en el 2000, alcanzan su máximo prácticamente al nacimiento. Por esta razón, para esta población costarricense su representación gráfica es estrictamente decreciente.

Número de años vividos desde el nacimiento hasta w: x + e_x

Si a la edad "x" de una persona se le suma su esperanza de vida a la edad se obtiene el número promedio de años que viviría, desde el nacimiento hasta su muerte. Gráficamente, esta nueva función toma la siguiente forma:

Para cualquier edad superior a cero el número de años que se espera viva una persona cualquiera es mayor que la esperanza de vida al nacer, pues ya supero el riesgo de morir en los años anteriores a su edad.

Relación de supervivencia: _nP_{x, x+n-1}

Las probabilidades de sobrevivencia, permiten obtener los sobrevivientes de un grupo de personas con edad cumplida "x". A diferencia de las probabilidades de sobrevivir _np_x que dependen únicamente de la edad inicial y del período "n", las relaciones de sobrevivencia dependen además del período que comprende la probabilidad "m". Si se desean determinar las relaciones de sobrevivencia para grupos quinquenales de edad, en períodos también de 5 años se tiene que la probabilidad de sobrevivir los siguientes 5 años para el grupo de personas con edades entre "x" y "x+n" se determina la razón entre los valores ₅L_x+5 entre ₅L_x:

La interpretación de esta razón corresponde a la probabilidad que tiene una persona de edad entre "x" y "x+n" en el año Z, de llegar con vida al año Z + 5.

Nuevamente los grupos extremos presentan problemas. Para la relación de sobrevivencia al nacimiento, debe considerarse la razón entre ₅L₀ con respecto a los nacimientos ocurridos en los 5 años 5l₀:

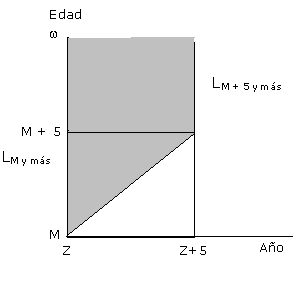
Esta relación hace referencia a la probabilidad que tienen las personas nacidas entre los años Z y Z + 4, de llegar con vida al año Z + 5.

Finalmente para el grupo abierto final se tiene que considerar un grupo adicional, si se está trabajando con el grupo de M y más, se debe considerar el grupo de M + 5 y más, pues la relación de sobrevivencia para el grupo se establece por:

Esta última relación permite determinar la probabilidad que, en el año Z, tiene una persona de edad M o más años, de sobrevivir los siguientes 5 años.

Estas relaciones tienen especial trascendencia cuando se desean realizar estimaciones y proyecciones de población, como bien se analizará más adelante.

Tarea de la sesión

Sesión anterior | siguiente